Frustrated Magnetism and Orbital Physics
Coupled Ladders and Chains
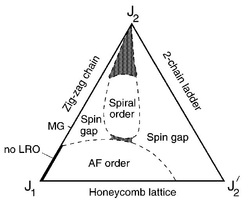
My involvement in frustrated magnetism grew first out of a materials problem in the search for S = 1/2 spin-ladder materials. A number of these, including SrCu2O3, have the "trellis lattice" structure, with a frustrated zig-zag coupling between the ladders. We mapped out [1] a triangular phase diagram which interpolates between the limits of ladders, chains and zig-zag chains, and used it [2] to place the CaV2O5 and MgV2O5 systems. We also suggested frustrated interchain coupling as a possible reason for the mysterious properties of (VO)2P2O7 [3].
Probing Frustrated Systems with Nonmagnetic Impurities
This topic [4-7] has its own separate page.
Extreme Frustration and High-Dimensional Spinons
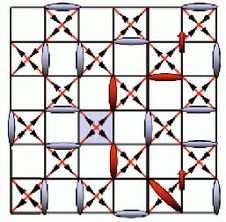
Our studies with nonmagnetic impurities [5] gave some hints that sufficiently highly frustrated systems could be associated with the presence of elementary S = 1/2 excitations (spinons) beyond one dimension. Some work on the square lattice with a frustration which makes the singlets and triplets of each elementary plaquette degenerate led to the concept of dimensional reduction. We put this Klein-type spin model on the checkerboard (2D) and pyrochlore (3D) lattices [8], where its ground state is spanned by the set of singlet dimer coverings and thus possesses an extensive ground-state degeneracy. This corresponds to complete dimensional reduction, i.e. to point-like excitations in the form of deconfined fractional spinons which propagate through the entire system.
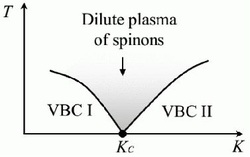
Although we showed that a Hubbard-type electronic model on the pyrochlore lattice can lie close to the Klein point, we also showed that, in two dimensions, this point is inherently unstable in that any perturbation restores spinon confinement at zero temperature. At finite temperatures, the deconfined phase survives as a dilute Coulomb gas of thermally excited spinons. At T = 0 and away from the Klein point, we used a variational approach based on the singlet dimer coverings of the pyrochlore lattice (and on dealing with their nonorthogonality) to show that the ground states are valence-bond crystal (VBC) phases. Our spinons can be considered as the quantum analogue of the classical "magnetic monopoles in pyrochlore antiferromagnets" which have received a lot of press since 2008.
Orbital Physics and Extreme Frustration
he physics of orbital degeneracy forms the basis for thescience and technology of colossal magnetoresistance in manganites. In fact it is a generic feature of all transition metals except for those at the edges of the sequence, and it adds a fundamental new parameter to the Hamiltonian of charge, spin and lattice degrees of freedom. My studies in orbital physics have been focussed on using orbital degeneracy to enhance frustration in magnetic systems, with the aim of finding liquid rather than ordered states. By this is meant states where spin and orbital order are sufficiently frustrated and unfavourable that the kinetic terms dominate instead, producing resonating ground states.
We decided that absolutely the most frustrated model realisable in a material must combine the geometrical frustration of the triangular lattice with the threefold orbital degeneracy of the t2g manifold and the quantum nature of S = 1/2 spins. This might be found on the <111> planes of NaTiO2 if structural distortion could be avoided. In a very long analysis of this model [11], we showed that ordered states are all very frustrated and spin-orbital dimer states are more favourable. We computed correlation functions for (very) small clusters and obtained energy gains due to resonance about valence-bond configurations (which are in fact exact in the direct-exchange limit of the model). However, we could not prove that the large resonance energies in the superexchange limit of the model would drive a spin-orbital liquid state. In a later analysis [12], I extracted quantum dimer models (QDMs) for the three cases of most interest, to find out if these might fall close to the known resonating valence-bond (RVB, liquid) states of triangular-lattice QDMs. I had a lot of fun playing with high-order hopping processes, multi-coloured QDM s, Majorana-fermion representations and triangular plaquette models, and I discovered the "colour vison" excitation, but in the end all the models lay far from the spin-liquid regime: they all favored local fluctuation processes about relatively small numbers of fixed VBC configurations.
Frustration: the Review Article
I was asked by Contemporary Physics to write an article making my work on frustrated systems accessible to an advanced undergraduate student. Unfortunately this was a little bit of an oxymoron, so instead I wrote a review article [13] focussing on the current (as of early 2009) hot topics in frustration, in the three different areas of
- materials: the preparation of frustrated systems;
- theory: the search for and characterisation of the spin liquid;
- numerics: the solution of frustrated models.
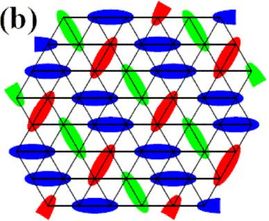
The S = 1/2 kagome Heisenberg antiferromagnet revisited
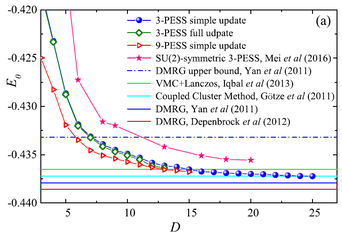
Despite many results, including our own, in favour of a gapped Z2 quantum spin-liquid ground state for the KHAF, contradictory signs were always present in other studies and questions always hung over the finite size of the systems investigated. The question at issue is extremely fundamental: is Anderson's paradigm of local, low-energy singlet units (dimers, plaquettes, ...), which gain further energy by resonating in space, the dominant physics ? Or is there another option, such as the algebraic spin liquid ? To find an unbiased method capable of answering this question, we spent some years developing the technique of tensor-network renormalisation from a nice concept to a quantitative numerical method. The physical keys here are first to find a method that works in infinite space, achieving its truncation in some other way, and second to recognise the fact that frustrated units have more than just pairwise entanglement, which needs to be handled by considering a simplex. Having developed the method of projected entangled simplex states (PESS) [14], we applied it to the Husimi lattice [15] to obtain both a numerical and a physical benchmark for the kagome problem. The Husimi lattice is a Bethe lattice of connected triangles that has exactly the local physics of the kagome lattice, but no loops. This means it can be handed very accurately by "simple-update" PESS, meaning that results can be obtained for very high bond dimensions, and they must also provide an upper limit for the kagome energy and ordered moment.
Despite many results, including our own, in favour of a gapped Z2 quantum spin-liquid ground state for the KHAF, contradictory signs were always present in other studies and questions always hung over the finite size of the systems investigated. The question at issue is extremely fundamental: is Anderson's paradigm of local, low-energy singlet units (dimers, plaquettes, ...), which gain further energy by resonating in space, the dominant physics ? Or is there another option, such as the algebraic spin liquid ? To find an unbiased method capable of answering this question, we spent some years developing the technique of tensor-network renormalisation from a nice concept to a quantitative numerical method. The physical keys here are first to find a method that works in infinite space, achieving its truncation in some other way, and second to recognise the fact that frustrated units have more than just pairwise entanglement, which needs to be handled by considering a simplex. Having developed the method of projected entangled simplex states (PESS) [14], we applied it to the Husimi lattice [15] to obtain both a numerical and a physical benchmark for the kagome problem. The Husimi lattice is a Bethe lattice of connected triangles that has exactly the local physics of the kagome lattice, but no loops. This means it can be handed very accurately by "simple-update" PESS, meaning that results can be obtained for very high bond dimensions, and they must also provide an upper limit for the kagome energy and ordered moment.
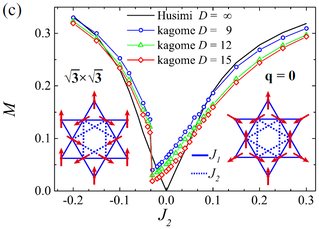
With these results in hand, and with some extra algorithmic development to maximise the bond dimension, we tackled the kagome problem ... and found algebraic behaviour [16]. An unconstrained solution finds ordered states at all finite bond dimensions, with the energy varying as a power law and the ordered moment vanishing in the limit of infinite bond dimension. This discovery of a gapless quantum spin liquid upends the Anderson paradigm, at least for systems whose simplices have odd-half-integer spin, in favour of a state where completely nonlocal spinons optimise their bandstructure in reciprocal space. In the meantime this type of state is also suspected on the J1-J2 square and triangular lattices. Confirmation from experiment is unlikely oto be forthcoming, due to materials difficulties (impurities and Dzyaloshinskii-Moriya interactions), but we did use PESS to investigate the stability of the gapless quantum spin liquid against the latter [17].
Triangular-lattice Heisenberg model
Another keystone model in frustrated quantum magnetism, and in fact Anderson's (misplaced) inspiration for the RVB state, is the S = 1/2 triangular-lattice antiferromagnet (TLAFM) with purely Heisenberg interactions. Ba8CoNb6O24
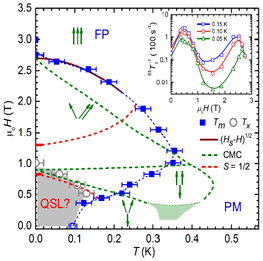
is a remarkable layered material whose Co ions have an effective spin 1/2 and construct a TLAFM with a very large interlayer spacing, ensuring purely two-dimensional character. We exploited this ideal realisation to perform a detailed experimental analysis of the S = 1/2 TLAFM [18]. First we found strong low-energy spin fluctuations and no magnetic ordering, but a diverging correlation length down to 0.1 K, indicating a Mermin-Wagner trend towards zero-temperature order. Below 0.1 K, however, our low-field measurements showed an unexpected magnetically disordered state, which is a candidate quantum spin liquid. We established the (H,T) phase diagram, mapping in detail the quantum fluctuation corrections to the available theoretical analysis. These included a strong upshift in field of the maximum ordering temperature, qualitative changes to both low- and high-field phase boundaries, and an ordered regime apparently dominated by the collinear “up-up-down” state. With Ba8CoNb6O24 we were therefore able to offer fresh input for the development of theoretical and numerical approaches to the field-induced quantum phase transitions of the S = 1/2 Heisenberg TLAFM, and this work is ongoing.
Another keystone model in frustrated quantum magnetism, and in fact Anderson's (misplaced) inspiration for the RVB state, is the S = 1/2 triangular-lattice antiferromagnet (TLAFM) with purely Heisenberg interactions. Ba8CoNb6O24
is a remarkable layered material whose Co ions have an effective spin 1/2 and construct a TLAFM with a very large interlayer spacing, ensuring purely two-dimensional character. We exploited this ideal realisation to perform a detailed experimental analysis of the S = 1/2 TLAFM [18]. First we found strong low-energy spin fluctuations and no magnetic ordering, but a diverging correlation length down to 0.1 K, indicating a Mermin-Wagner trend towards zero-temperature order. Below 0.1 K, however, our low-field measurements showed an unexpected magnetically disordered state, which is a candidate quantum spin liquid. We established the (H,T) phase diagram, mapping in detail the quantum fluctuation corrections to the available theoretical analysis. These included a strong upshift in field of the maximum ordering temperature, qualitative changes to both low- and high-field phase boundaries, and an ordered regime apparently dominated by the collinear “up-up-down” state. With Ba8CoNb6O24 we were therefore able to offer fresh input for the development of theoretical and numerical approaches to the field-induced quantum phase transitions of the S = 1/2 Heisenberg TLAFM, and this work is ongoing.
Maximal Frustration:
We instigated a project to investigate the properties of perfectly frustrated models, where flat magnon bands offer unconventional physics and a disappearance of the QMC sign problem offers numerical possibilities usually excluded for frustrated systems. We discovered extreme localisation, multiparticle bound states, anomalous densities of states and thermodynamic properties, first-order quantum phase transitions and finite-temperature critical points [19-25], all of which are enough for this topic to merit its own separate page.
We instigated a project to investigate the properties of perfectly frustrated models, where flat magnon bands offer unconventional physics and a disappearance of the QMC sign problem offers numerical possibilities usually excluded for frustrated systems. We discovered extreme localisation, multiparticle bound states, anomalous densities of states and thermodynamic properties, first-order quantum phase transitions and finite-temperature critical points [19-25], all of which are enough for this topic to merit its own separate page.
Further Forms of Frustration
Frustration can involve a lot more than merely competing Heisenberg spin interactions. Without taking the definition too broadly, three further pieces of work can be classified in this section.
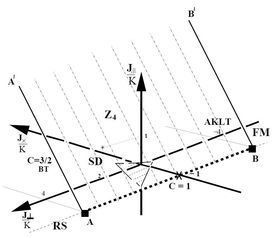
i) The cyclic ring-exchange interaction on a four-site plaquette is non-negligible in cuprate materials and competes with Heisenberg interactions to form a number of different types of ordered phase, including spontanously dimerised, scalar chiral and vector chiral. We investigated these states, and the quantum phase transitions between them, in a spin ladder [26]. We used the existence of a number of exactly soluble points in a slightly generalised Hamiltonian to draw the complete phase diagram and to conduct a detailed analysis of the effects of ring-exchange terms in this one-dimensional chain of plaquettes.
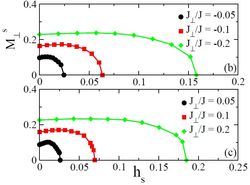
ii) Effective staggered magnetic field terms can arise in a spin system due to Dyzaloshinskii-Moriya interactions or g-tensor anisotropies. We used quantum Monte Carlo simulations of coupled spin chains to analyse the competition of the field term with the Heisenberg interactions, studying the transverse moment of the ordered phases and the gap of the disordered ones. We found some novel enhancement of magnetic order by a competing field at low interchain coupling and quasi-one-dimensionality at high coupling in a field of sufficient strength [27].
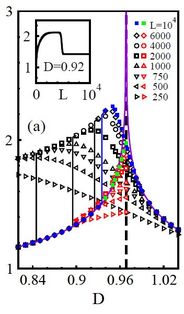
iii) The single-ion anisotropy D of spins with S > 1/2 also competes with Heisenberg interactions, preferring to form a nonmagnetic or low-spin state. For S = 1, the Gaussian transition from the Haldane to the large-D phase has been a long-running saga on which many authors have tested different techniques. We used [28] an improved DMRG algorithm which controls the absolute (rather than relative) error very strictly, and applied it to the bulk entropy of the system to fix the transition at D/J = 0.96845(8). With this we calculated the ground-state energy, gap, velocity, transverse string-order parameter, Luttinger parameter and critical exponent to extremely high accuracy. We used our results to deduce quantitatively the logarithmic divergence of the entropy at the critical point and confirm the topological nature of the transition.
Proximate Kitaev Physics
The richest form of alternative frustration introduced this century is Kitaev's exactly soluble bond-selective Ising model. We started to follow this field in order to interpret experimental results for some candidate Kitaev materials [29,30] and then developed the theory of models proximate to the Kitaev phase in the lextended phase diagram of 4d and 5d systems. This led us to a new gapless quantum spin-liquid state and to new forms of topology [31,32], which are described on a separate page.
The richest form of alternative frustration introduced this century is Kitaev's exactly soluble bond-selective Ising model. We started to follow this field in order to interpret experimental results for some candidate Kitaev materials [29,30] and then developed the theory of models proximate to the Kitaev phase in the lextended phase diagram of 4d and 5d systems. This led us to a new gapless quantum spin-liquid state and to new forms of topology [31,32], which are described on a separate page.
[1] Phase Diagram of the S = 1/2 Frustrated Coupled Ladder System,
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[2] Magnetic Properties of the Coupled Ladder System MgV2O5,
P.Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[3] Magnetic Properties of (VO)2P2O7 from Frustrated Interchain Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 58, R14705 (1998).
[4] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets,
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[5] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[6] Nonmagnetic Impurities in the S = 3/2 Kagome Antiferromagnet,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[7] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2,
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
[8] High-dimensional Fractionalization and Spinon Deconfinement in Pyrochlore Antiferromagnets
Z. Nussinov, B. Normand, C. D. Batista and S. A. Trugman,
Phys. Rev. B 75, 094411 (2007).
[9] Hubbard Model on the Pyrochlore Lattice: a 3D Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. Lett. 112, 207202 (2014).
[10] Fermionic Spinon and Holon Statistics in the Pyrochlore Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. B 93, 115122 (2016).
[11] Frustration and Entanglement in the t2g Spin-Orbital Model on the Triangular Lattice:
Valence-Bond and Generalized Liquid States,
B. Normand and A. M. Oleś,
Phys. Rev. B 78, 094427 (2008).
[12] Multicolored Quantum Dimer Models, Resonating Valence-Bond States, Color Visons, and
the Triangular-Lattice t2g Spin-Orbital System,
B. Normand,
Phys. Rev. B 83, 064413 (2011).
[13] Frontiers in Frustrated Magnetism,
B. Normand,
Contemporary Physics 50, 4, 533 (2009).
[14] Tensor Renormalization of Quantum Many-Body Systems using Projected Entangled Simplex States,
Z. Y. Xie, J. Chen, J. F. Yu, X. Kong, B. Normand and T. Xiang,
Phys. Rev. X 4, 011025 (2014).
[15] Heisenberg Antiferromagnet on the Husimi Lattice,
H. J. Liao, Z. Y. Xie, J. Chen, X. J. Han, H. D. Xie, B. Normand and T. Xiang,
Phys. Rev. B 93, 075154 (2016).
[16] Gapless Spin-Liquid Ground State in the S = 1/2 Kagome Antiferromagnet,
H. J. Liao, Z. Y. Xie, J. Chen, X. Kong, B. Normand and T. Xiang,
Phys. Rev. Lett. 118, 137202 (2017).
[17] Gapless Spin Liquid in the Kagome Heisenberg Antiferromagnet with Dzyaloshinskii-Moriya
Interactions,
C.-Y. Lee, B. Normand and Y.-J. Kao,
Phys. Rev. B 98, 224414 (2018).
[18] Mermin-Wagner Physics, (H, T) Phase Diagram, and Candidate Quantum Spin-Liquid Phase
in the Spin-1/2 Triangular-Lattice Antiferromagnet Ba8CoNb6O24,
Y. Cui, J. Dai, P. Zhou, P. S. Wang, T. R. Li, W. H. Song, L. Ma, Z. Zhang, S. Y. Li, G. M. Luke,
B. Normand, T. Xiang and W. Yu,
Phys. Rev. Mater. 2, 044403 (2018).
[19] Thermodynamic Properties of Highly Frustrated Quantum Spin Ladders: Influence of
Many-Particle Bound States,
A. Honecker, S. Wessel, R. Kerkdyk, T. Pruschke, F. Mila and B. Normand,
Phys. Rev. B 93, 054408 (2016).
[20] Multi-Triplet Bound States and Finite-Temperature Dynamics in Highly Frustrated Quantum
Spin Ladders,
A. Honecker, F. Mila and B. Normand,
Phys. Rev. B 94, 094402 (2016).
[21] Efficient Quantum Monte-Carlo Simulations of Highly Frustrated Magnets: the Frustrated
Spin-1/2 Ladder,
S. Wessel, B. Normand, F. Mila and A. Honecker,
SciPost Phys. 3, 005 (2017).
[22] Thermal Critical Points and Quantum Critical End Point in the Frustrated Bilayer Heisenberg
Antiferromagnet,
J. Stapmanns, P. Corboz, F. Mila, A. Honecker, B. Normand and S. Wessel,
Phys. Rev. Lett. 121, 127201 (2018).
[23] Thermodynamic Properties of the Shastry-Sutherland Model from Quantum Monte Carlo Simulations,
S. Wessel, I. Niesen, J. Stapmanns, B. Normand, F. Mila, P. Corboz and A. Honecker,
Phys. Rev. B 98, 174432 (2018).
[24] Thermodynamic Properties of the Shastry-Sutherland Model throughout the Dimer-Product Phase,
A. Wietek, P. Corboz, S. Wessel, B. Normand, F. Mila and A. Honecker,
Phys. Rev. Res. 1, 033038 (2019).
[25] A Quantum Magnetic Analogue to the Critical Point of Water,
J. Larrea Jiménez, S. P. G. Crone, E. Fogh, M. Zayed, R. Lortz, E. Pomjakushina, K. Conder,
A. M. Läuchli, L. Weber, S. Wessel, A. Honecker, B. Normand, Ch. Rüegg, P. Corboz, H. M.
Rønnow and F. Mila,
unpublished (arXiv:2009.14492).
[26] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[27] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in
Staggered Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[28] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 224402 (2011).
[29] Anomalous Thermal Conductivity and Magnetic Torque Response in the Honeycomb Magnet RuCl3,
I. A. Leahy, C. A. Pocs, P. E. Siegfried, D. Graf, S.-H. Do, K.-Y. Choi, B. Normand and M. Lee,
Phys. Rev. Lett. 118, 187203 (2017).
[30] Gapless Spin Excitations in the Field-Induced Quantum Spin-Liquid Phase of RuCl3,
J. Zheng, K. Ran, T. Li, J. Wang, P. Wang, B. Liu, Z.-X. Liu, B. Normand, J. Wen and W. Yu,
Phys. Rev. Lett. 119, 227208 (2017).
[31] Dirac and Chiral Quantum Spin Liquids on the Honeycomb Lattice in a Magnetic Field,
Z.-X. Liu and B. Normand,
Phys. Rev. Lett. 120, 187201 (2018).
[32] One Proximate Kitaev Spin Liquid in the K-J-Γ Model on the Honeycomb Lattice,
J. Wang, B. Normand and Z.-X. Liu,
Phys. Rev. Lett. 123, 197201 (2019).
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[2] Magnetic Properties of the Coupled Ladder System MgV2O5,
P.Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[3] Magnetic Properties of (VO)2P2O7 from Frustrated Interchain Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 58, R14705 (1998).
[4] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets,
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[5] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[6] Nonmagnetic Impurities in the S = 3/2 Kagome Antiferromagnet,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[7] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2,
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
[8] High-dimensional Fractionalization and Spinon Deconfinement in Pyrochlore Antiferromagnets
Z. Nussinov, B. Normand, C. D. Batista and S. A. Trugman,
Phys. Rev. B 75, 094411 (2007).
[9] Hubbard Model on the Pyrochlore Lattice: a 3D Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. Lett. 112, 207202 (2014).
[10] Fermionic Spinon and Holon Statistics in the Pyrochlore Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. B 93, 115122 (2016).
[11] Frustration and Entanglement in the t2g Spin-Orbital Model on the Triangular Lattice:
Valence-Bond and Generalized Liquid States,
B. Normand and A. M. Oleś,
Phys. Rev. B 78, 094427 (2008).
[12] Multicolored Quantum Dimer Models, Resonating Valence-Bond States, Color Visons, and
the Triangular-Lattice t2g Spin-Orbital System,
B. Normand,
Phys. Rev. B 83, 064413 (2011).
[13] Frontiers in Frustrated Magnetism,
B. Normand,
Contemporary Physics 50, 4, 533 (2009).
[14] Tensor Renormalization of Quantum Many-Body Systems using Projected Entangled Simplex States,
Z. Y. Xie, J. Chen, J. F. Yu, X. Kong, B. Normand and T. Xiang,
Phys. Rev. X 4, 011025 (2014).
[15] Heisenberg Antiferromagnet on the Husimi Lattice,
H. J. Liao, Z. Y. Xie, J. Chen, X. J. Han, H. D. Xie, B. Normand and T. Xiang,
Phys. Rev. B 93, 075154 (2016).
[16] Gapless Spin-Liquid Ground State in the S = 1/2 Kagome Antiferromagnet,
H. J. Liao, Z. Y. Xie, J. Chen, X. Kong, B. Normand and T. Xiang,
Phys. Rev. Lett. 118, 137202 (2017).
[17] Gapless Spin Liquid in the Kagome Heisenberg Antiferromagnet with Dzyaloshinskii-Moriya
Interactions,
C.-Y. Lee, B. Normand and Y.-J. Kao,
Phys. Rev. B 98, 224414 (2018).
[18] Mermin-Wagner Physics, (H, T) Phase Diagram, and Candidate Quantum Spin-Liquid Phase
in the Spin-1/2 Triangular-Lattice Antiferromagnet Ba8CoNb6O24,
Y. Cui, J. Dai, P. Zhou, P. S. Wang, T. R. Li, W. H. Song, L. Ma, Z. Zhang, S. Y. Li, G. M. Luke,
B. Normand, T. Xiang and W. Yu,
Phys. Rev. Mater. 2, 044403 (2018).
[19] Thermodynamic Properties of Highly Frustrated Quantum Spin Ladders: Influence of
Many-Particle Bound States,
A. Honecker, S. Wessel, R. Kerkdyk, T. Pruschke, F. Mila and B. Normand,
Phys. Rev. B 93, 054408 (2016).
[20] Multi-Triplet Bound States and Finite-Temperature Dynamics in Highly Frustrated Quantum
Spin Ladders,
A. Honecker, F. Mila and B. Normand,
Phys. Rev. B 94, 094402 (2016).
[21] Efficient Quantum Monte-Carlo Simulations of Highly Frustrated Magnets: the Frustrated
Spin-1/2 Ladder,
S. Wessel, B. Normand, F. Mila and A. Honecker,
SciPost Phys. 3, 005 (2017).
[22] Thermal Critical Points and Quantum Critical End Point in the Frustrated Bilayer Heisenberg
Antiferromagnet,
J. Stapmanns, P. Corboz, F. Mila, A. Honecker, B. Normand and S. Wessel,
Phys. Rev. Lett. 121, 127201 (2018).
[23] Thermodynamic Properties of the Shastry-Sutherland Model from Quantum Monte Carlo Simulations,
S. Wessel, I. Niesen, J. Stapmanns, B. Normand, F. Mila, P. Corboz and A. Honecker,
Phys. Rev. B 98, 174432 (2018).
[24] Thermodynamic Properties of the Shastry-Sutherland Model throughout the Dimer-Product Phase,
A. Wietek, P. Corboz, S. Wessel, B. Normand, F. Mila and A. Honecker,
Phys. Rev. Res. 1, 033038 (2019).
[25] A Quantum Magnetic Analogue to the Critical Point of Water,
J. Larrea Jiménez, S. P. G. Crone, E. Fogh, M. Zayed, R. Lortz, E. Pomjakushina, K. Conder,
A. M. Läuchli, L. Weber, S. Wessel, A. Honecker, B. Normand, Ch. Rüegg, P. Corboz, H. M.
Rønnow and F. Mila,
unpublished (arXiv:2009.14492).
[26] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[27] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in
Staggered Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[28] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 224402 (2011).
[29] Anomalous Thermal Conductivity and Magnetic Torque Response in the Honeycomb Magnet RuCl3,
I. A. Leahy, C. A. Pocs, P. E. Siegfried, D. Graf, S.-H. Do, K.-Y. Choi, B. Normand and M. Lee,
Phys. Rev. Lett. 118, 187203 (2017).
[30] Gapless Spin Excitations in the Field-Induced Quantum Spin-Liquid Phase of RuCl3,
J. Zheng, K. Ran, T. Li, J. Wang, P. Wang, B. Liu, Z.-X. Liu, B. Normand, J. Wen and W. Yu,
Phys. Rev. Lett. 119, 227208 (2017).
[31] Dirac and Chiral Quantum Spin Liquids on the Honeycomb Lattice in a Magnetic Field,
Z.-X. Liu and B. Normand,
Phys. Rev. Lett. 120, 187201 (2018).
[32] One Proximate Kitaev Spin Liquid in the K-J-Γ Model on the Honeycomb Lattice,
J. Wang, B. Normand and Z.-X. Liu,
Phys. Rev. Lett. 123, 197201 (2019).
