Further Projects
Magnetoelastic Coupling in (VO)2P2O7
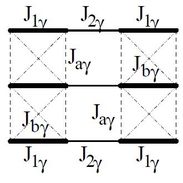
Vanadyl pyrophosphate [(VO)2P2O7, or VOPO] is a black powder of considerable industrial importance as a catalyst for methanol production, and a reliable source informs the author that DuPont has a VOPO factory somewhere in Spain. For the physicist, theorist or experimentalist, the more one looks at VOPO, the more one finds. It is a system of dimerised chains (not ladders) of S = 1/2 V(4+) ions. Our early work [1] showed that, assuming a purely magnetic Hamiltonian, the thermodynamic and dynamic measurements could only be explained by a significant, and frustrating, interchain coupling.
Detailed NMR and neutron scattering experiments
then found that a consistent explanation would need a rather complex magnetic structure. Raman light scattering measurements indicated in addition a strong magnetoelastic coupling. Thus we presented qualitative arguments [2] for why the extremely small structural distortions should have such significant magnetic effects, and combined these with a study of the coupled spin and lattice systems. Using the theoretical method of continuous unitary transformations (CUTs), in which the respective magnon and phonon excitations are separated and transformed systematically, we found good qualitative and quantitative agreement with all the thermodynamic quantities already measured for the material. We also predicted the finite-temperature dynamical properties, namely thermal renormalisation of the magnon dispersion by phonons, which as far as we know still await measurement.
then found that a consistent explanation would need a rather complex magnetic structure. Raman light scattering measurements indicated in addition a strong magnetoelastic coupling. Thus we presented qualitative arguments [2] for why the extremely small structural distortions should have such significant magnetic effects, and combined these with a study of the coupled spin and lattice systems. Using the theoretical method of continuous unitary transformations (CUTs), in which the respective magnon and phonon excitations are separated and transformed systematically, we found good qualitative and quantitative agreement with all the thermodynamic quantities already measured for the material. We also predicted the finite-temperature dynamical properties, namely thermal renormalisation of the magnon dispersion by phonons, which as far as we know still await measurement.
Charge Order in Manganites
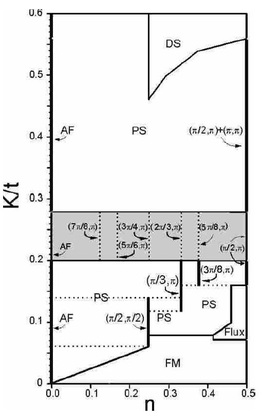
Colossal magnetoresistive (CMR) manganites form the basis for a large amount of both fundamental science and technological application. The observation of charge-inhomogeneous stripe ordering in two classes of manganites made us investigate this phenomenon [3] within the general but minimal "Ferromagnetic Kondo Lattice model:" manganites are characterised by the competition between a double-exchange hopping interaction, t, driven by the kinetics of the conduction electrons and favouring ferromagnetic core-spin alignment, and a superexchange, J, between these core spins which favours antiferromagnetism. We analysed the ground-state spin and charge configurations using a self-consistent combination of analytical expressions for the conduction-electron contribution and classical Monte Carlo simulations for the core spins, to map out the phase diagram in J/t and the filling, x. We found a wide variety of novel charge "island" phases and spin-flux phases, with wide regions of phase separation among these. Most of the island phases indeed have striped charge order, indicating that the basic features of the materials may already be traced to the fundamental competition of t and J.
Solution Physics
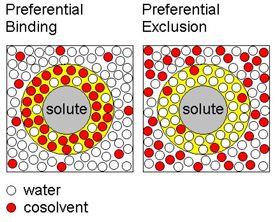
The solvation of non-polar molecules in a polar solvent like water is both a complex problem in the physics of hydrogen bonding and a process fundamental to a bunch of industries, to cooking, to the function of soap and indeed to a number of biological processes which sustain life itself. Some of my colleagues had a very elegant model based only on the energy and entropy of the water molecules in a shell next to the polar surface, and how these compared to their energy in the bulk solvent (the energy goes up but the entropy comes down). We used this to show how further results in the solution physics of hydrophobic molecules energe naturally. One was the formation in solution of ordered structures -- micelles -- of soap-like molecules, those with a polar head but long, non-polar tails [4]. The other was the action of "third-party" cosolvent molecules which can alter the solution process of the non-polar species: they do this by interfering with (enhancing or scrambling) the structure of the bulk solvent, changing these energy and entropy terms and thus altering the balance in temperature and concentration where the large molecule can be dissolved [5].
Ionic Hubbard Model
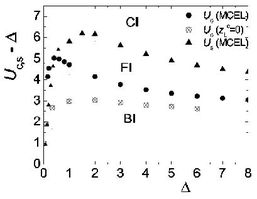
The ionic Hubbard model is the minimal model for the transition from a band insulator (dictated by one-particle energy terms) to a Mott insulator (dictated by electron interaction terms). It has a generalisation away from half-filling which should remove the Umklapp terms and might create metallic rather than insulating phases. However, we investigated the phase diagram [6] for three- and four-site unit cells and found that it has the same generic properties as the two-site version, albeit more weakly and as a consequence of generated interaction terms. These properties are a band insulator (BI) for large ionicity separated from a (Mott-like) correlated insulator (CI) for large on-site repulsion by an intermediate phase (FI) notable for spontaneous symmetry breaking in its bond-order, which makes it ferroelectric and gives it fractional quasiparticles with an incommensurate (interaction-tunable) fraction.
Cold Bosons in a Trap
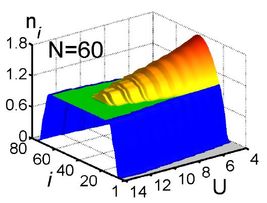
The preparation of condensates of ultra-cold atoms in tunable potentials has truly opened up a whole new chapter in many-body physics. We wanted to investigate exactly how the superfluid phase at low interaction strength, U,
goes over to the Mott insulator phase at high U in an experiment. Because these are done by first trapping a fixed number of atoms, the ensemble is canonical rather than grand-canonical, and the presence of 3 energy scales (U, the kinetic term, t, the trap term, V) implies 2 energy ratios, 2 transitions and 3 phases. We studied this process [7] for interacting bosons on an optical lattice in a one-dimensional, harmonic trap by high-precision DMRG calculations. We indeed found an intermediate regime between the SF and the MI, characterised by a cascade of microscopic steps. These steps are a consequence of individual boson ``squeezing'' events, where atoms are pushed from the centre to the edge of the trap with increasing U, and they even show an even-odd alternation which depends on how the trap is centred relative to the optical lattice. This sort of behaviour is quite generic in an external trap, and we calculated the parameters for observing it.
goes over to the Mott insulator phase at high U in an experiment. Because these are done by first trapping a fixed number of atoms, the ensemble is canonical rather than grand-canonical, and the presence of 3 energy scales (U, the kinetic term, t, the trap term, V) implies 2 energy ratios, 2 transitions and 3 phases. We studied this process [7] for interacting bosons on an optical lattice in a one-dimensional, harmonic trap by high-precision DMRG calculations. We indeed found an intermediate regime between the SF and the MI, characterised by a cascade of microscopic steps. These steps are a consequence of individual boson ``squeezing'' events, where atoms are pushed from the centre to the edge of the trap with increasing U, and they even show an even-odd alternation which depends on how the trap is centred relative to the optical lattice. This sort of behaviour is quite generic in an external trap, and we calculated the parameters for observing it.
Potts Models on Irregular Lattices
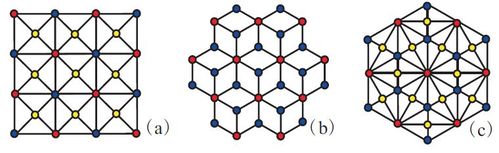
Potts models are an excellent example of classical statistical mechanics at high entropies. A curiously large number of Potts models with a value of the site "direction," q, somehow corresponding to the connectivity of the lattice, z, order only at T = 0. However, the q = 3 Potts model on the diced lattice (b) is an exception here, ordering at a finite temperature. We were working on applications of tensor-based numerical methods in classical systems and decided to investigate this type of transition by finding another such "exception." The Union-Jack lattice (a), like the diced lattice, is "irregular" in the sense that there are different types of site with different coordination numbers. We evaluated [8] the thermodynamic properties (entropy, specific heat, "magnetisation," susceptibility) of the 4-state antiferromagnetic Potts model on the Union-Jack lattice and found a previously unknown, ``entropy-driven,'' finite-temperature phase transition to a partially ordered state, similar to that in the diced lattice. With this insight we also computed the thermodynamics of Potts models on the diced and centred diced (c) lattices, the latter a third example in this class, and suggested that finite-temperature transitions and partially ordered states are ubiquitous on irregular lattices. Later we completed a more detailed investigation of these phenomena to make their connection with lattice irregularity as systematic as possible [9].
Two-Dimensional Materials: Black Phosphorous
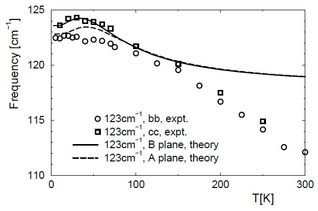
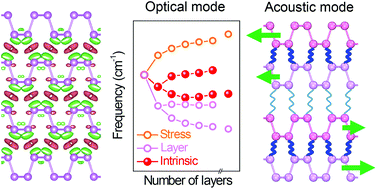
Stacking two-dimensional (2D) materials into multi-layers or heterostructures, known as van der Waals (vdW) epitaxy, is an essential degree of freedom for tuning their properties on demand. Few-layer black phosphorus (FLBP), a material with high potential for nano- and optoelectronics applications, appears to have interlayer couplings much stronger than graphene and other 2D systems. Indeed, these couplings call into question whether the stacking of FLBP can be governed only by vdW interactions, which is of crucial importance for epitaxy and property refinement. We performed a theoretical investigation of the vibrational properties of FLBP [10], which reflect directly its interlayer coupling, by discussing six Raman-observable phonons, including three optical, one breathing and two shear modes. By increasing the thickness of the FLBP system, we found anomalous redshifts of the frequencies for each optical mode but a blueshift for the armchair shear mode. Our calculations also showed splitting of the phonon branches, arising due to anomalous surface phenomena, and strong phonon-phonon coupling. By computing uniaxial stress effects, inter-atomic force constants and electron densities, we demonstrated that these properties are the consequence of strong and highly directional interlayer interactions arising from the electronic hybridisation of the lone electron-pairs of FLBP, rather than from vdW interactions. This exceptional interlayer coupling mechanism controls the stacking stability in BP, and in a more general context it opens a new avenue beyond vdW epitaxy for understanding the design of 2D heterostructures.
Stacking two-dimensional (2D) materials into multi-layers or heterostructures, known as van der Waals (vdW) epitaxy, is an essential degree of freedom for tuning their properties on demand. Few-layer black phosphorus (FLBP), a material with high potential for nano- and optoelectronics applications, appears to have interlayer couplings much stronger than graphene and other 2D systems. Indeed, these couplings call into question whether the stacking of FLBP can be governed only by vdW interactions, which is of crucial importance for epitaxy and property refinement. We performed a theoretical investigation of the vibrational properties of FLBP [10], which reflect directly its interlayer coupling, by discussing six Raman-observable phonons, including three optical, one breathing and two shear modes. By increasing the thickness of the FLBP system, we found anomalous redshifts of the frequencies for each optical mode but a blueshift for the armchair shear mode. Our calculations also showed splitting of the phonon branches, arising due to anomalous surface phenomena, and strong phonon-phonon coupling. By computing uniaxial stress effects, inter-atomic force constants and electron densities, we demonstrated that these properties are the consequence of strong and highly directional interlayer interactions arising from the electronic hybridisation of the lone electron-pairs of FLBP, rather than from vdW interactions. This exceptional interlayer coupling mechanism controls the stacking stability in BP, and in a more general context it opens a new avenue beyond vdW epitaxy for understanding the design of 2D heterostructures.
Type-II Multiferroics
Type-II multiferroic materials are those in which the ferroelectric polarisation is driven by the (inversion-nonsymmetric) magnetic order, rather than being a charge-driven property. The interest in this class of materials is based on the promise of new and highly efficient multifunctional applications based on the mutual control of magnetic and electric properties.We investigated the origin of multiferroic behaviour in FeVO4 by NMR [11], finding no magnetic order near the Curie-Weiss temperature (116 K) and only short-ranged order below 65 K, but.two magnetic transitions at temperatures TN1 ≈ 19 K and TN2 ≈ 13 K. In the low-temperature incommensurate spiral state, we found the maximum ordered moment to be 1.95 μB/Fe, or only 1/3 of the local moment, and evidence for strong low-energy spin fluctuations in the unconventional power-law temperature dependence of 1/T1. The large Weiss constant, short-range magnetic correlations far above TN1, small ordered moment, significant low-energy spin fluctuations and incommensurate ordered phases all provided explicit evidence for strong magnetic frustration in FeVO4, pointing unequivocally to type-II multiferroicity.
Type-II multiferroic materials are those in which the ferroelectric polarisation is driven by the (inversion-nonsymmetric) magnetic order, rather than being a charge-driven property. The interest in this class of materials is based on the promise of new and highly efficient multifunctional applications based on the mutual control of magnetic and electric properties.We investigated the origin of multiferroic behaviour in FeVO4 by NMR [11], finding no magnetic order near the Curie-Weiss temperature (116 K) and only short-ranged order below 65 K, but.two magnetic transitions at temperatures TN1 ≈ 19 K and TN2 ≈ 13 K. In the low-temperature incommensurate spiral state, we found the maximum ordered moment to be 1.95 μB/Fe, or only 1/3 of the local moment, and evidence for strong low-energy spin fluctuations in the unconventional power-law temperature dependence of 1/T1. The large Weiss constant, short-range magnetic correlations far above TN1, small ordered moment, significant low-energy spin fluctuations and incommensurate ordered phases all provided explicit evidence for strong magnetic frustration in FeVO4, pointing unequivocally to type-II multiferroicity.
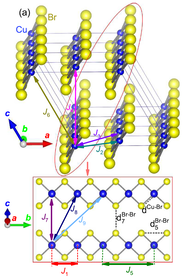
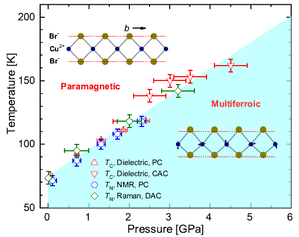
Although type-II multiferroicity has to date been limited to low temperatures, especially in non-oxide materials, we discovered a giant pressure-dependence of the multiferroic critical temperature in CuBr2 [12]. At 4.5 GPa, TC was enhanced from 73.5 to 162 K. This growth showed no sign of saturating and the dielectric loss remained small under these high pressures. We established the structure under pressure and demonstrated a 60% increase in the two-magnon Raman energy scale up to 3.6 GPa. We then performed first-principles structural and magnetic energy calculations to provide a quantitative explanation for these results in terms of dramatically pressure-enhanced interactions between CuBr2
chains. These large, pressure-tuned magnetic interactions definitely suggest structural control in cuprous halides as a route to applied high-temperature multiferroicity.
chains. These large, pressure-tuned magnetic interactions definitely suggest structural control in cuprous halides as a route to applied high-temperature multiferroicity.
Thermal Conductivity
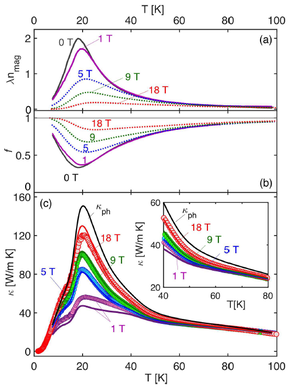
Insulating quantum magnets lie at the forefront not only of fundamental research into quantum matter but also of technological exploitation in the increasingly applied field of spintronics. The magnetic thermal transport is a particularly sensitive probe of the elementary spin and exotic topological excitations in unconventional magnetic materials. However, magnetic contributions to heat conduction are invariably intertwined with lattice (phonon) contributions, and thus the issue of spin-phonon coupling in determining the spin and thermal transport properties of magnetic insulators becomes more important with every emergent topological magnetic system. While investigating this interplay in the layered honeycomb material CrCl3, we discovered an anomalously strong enhancement of the thermal conductivity, occurring at all relevant temperatures, in the presence of an applied magnetic field. Away from the magnetically ordered phase at low temperatures and small fields, there is no coherent spin contribution to the thermal conductivity, and hence this effect must be caused by strong suppression of the phonon thermal conductivity due to magnetic fluctuations, which are in turn suppressed by the field. We built an empirical model for the thermal conductivity of CrCl3 within a formalism assuming an independently determined number of spin-flip processes and an efficiency of the phonon scattering events they mediate. By extracting the intrinsic phonon thermal conductivity, we obtained a quantitative description of our measured data at all fields and temperatures, within which we could demonstrate that the scattering efficiency is entirely independent of the applied field. In this way, we used CrCl3 as a model system to formulate a quite general framework for describing the interactions between spin and phonon excitations in the context of thermal transport in magnetic quantum materials.
Insulating quantum magnets lie at the forefront not only of fundamental research into quantum matter but also of technological exploitation in the increasingly applied field of spintronics. The magnetic thermal transport is a particularly sensitive probe of the elementary spin and exotic topological excitations in unconventional magnetic materials. However, magnetic contributions to heat conduction are invariably intertwined with lattice (phonon) contributions, and thus the issue of spin-phonon coupling in determining the spin and thermal transport properties of magnetic insulators becomes more important with every emergent topological magnetic system. While investigating this interplay in the layered honeycomb material CrCl3, we discovered an anomalously strong enhancement of the thermal conductivity, occurring at all relevant temperatures, in the presence of an applied magnetic field. Away from the magnetically ordered phase at low temperatures and small fields, there is no coherent spin contribution to the thermal conductivity, and hence this effect must be caused by strong suppression of the phonon thermal conductivity due to magnetic fluctuations, which are in turn suppressed by the field. We built an empirical model for the thermal conductivity of CrCl3 within a formalism assuming an independently determined number of spin-flip processes and an efficiency of the phonon scattering events they mediate. By extracting the intrinsic phonon thermal conductivity, we obtained a quantitative description of our measured data at all fields and temperatures, within which we could demonstrate that the scattering efficiency is entirely independent of the applied field. In this way, we used CrCl3 as a model system to formulate a quite general framework for describing the interactions between spin and phonon excitations in the context of thermal transport in magnetic quantum materials.
[1] Magnetic Properties of (VO)2P2O7 from Frustrated Interchain Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 58, R14705 (1998).
[2] Magnetic Properties of (VO)2P2O7: Two-Plane Structure and Spin-Phonon Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 63, 134418 (2001).
[3] Island Phases and Charge Order in Two-Dimensional Manganites,
H. Aliaga, B. Normand, K. Hallberg, M. Avignon and B. Alascio,
Phys. Rev. B 64, 024422 (2001).
[4] Solvent-Induced Micelle Formation in a Hydrophobic Interaction Model,
S. Moelbert, B. Normand and P. de los Rios,
Phys. Rev. E 69, 061924 (2004).
[5] Cosmotropes and Chaotropes: Modelling Preferential Exclusion, Binding and Aggregate Stability
S. Moelbert, B. Normand and P. de los Rios,
Biophys. Chem. 112, 45 (2004)
[6] Quantum Phase Diagram of the Generalized Ionic Hubbard Model for ABn Chains,
M. E. Torio, A. A. Aligia, G. I. Japaridze and B. Normand,
Phys. Rev. B 73, 115109 (2006).
[7] Quantized Squeezing and Even-Odd Asymmetry of Trapped Bosons,
S. Hu, Y. C. Wen, Y. Yu, B. Normand and X. Q. Wang,
Phys. Rev. A 80, 063624 (2009).
[8] Finite-Temperature Phase Transitions in Potts Models on Irregular Lattices,
Q. N. Chen, M. P. Qin, J. Chen, Z. C. Wei, H. H. Zhao, B. Normand and T. Xiang,
Phys. Rev. Lett. 107, 165701 (2011).
[9] Partial Long–Range Order in Antiferromagnetic Potts Models,
M. P. Qin, Q. N. Chen, J. Chen, Z. C. Wei, H. H. Zhao, B. Normand and T. Xiang,
Phys. Rev. B 90, 144424 (2014).
[10] Interlayer Electronic Hybridization leads to Exceptional Thickness-Dependent Vibrational
Properties in Few-Layer Black Phosphorus,
Z.-X. Hu, X.-H. Kong, J.-S. Qiao, B. Normand and W. Ji,
Nanoscale 8, 2740 (2016).
[11] Spin Fluctuations and Frustrated Magnetism in the Multiferroic FeVO4,
J. Zhang, L. Ma, J. Dai, Y. P. Zhang, Z. Z. He, B. Normand and W. Q. Yu,
Phys. Rev. B 89, 174412 (2014).
[12] Giant Pressure-Enhancement of Multiferroicity in CuBr2,
J.-S. Zhang, Y. Xie, X. Q. Liu, A. Razpopov, V. Borisov, C. Wang, J. P. Sun, Y. Cui, J. C. Wang,
X. Ren, H. Deng, X. Yin, Y. Ding, Y. Li, J. G. Cheng, J. Feng, R. Valentí, B. Normand and W. Yu,
Phys. Rev. Res. 2, 013144 (2020).
[13] Giant Thermal Magnetoconductivity in CrCl3 and a General Model for Spin-Phonon Scattering,
C. Pocs, I. Leahy, H. Zheng, G. Cao, E.-S. Choi, S.-H. Do, K.-Y. Choi, B. Normand and M. Lee,
Phys. Rev. Res. 2, 013059 (2020).
