Nonmagnetic Impurities in Quantum Magnets
Impurity doping is a valuable probe of underlying spin correlations, which are otherwise difficult to observe, in a quantum ground state. Most experimental and theoretical investigation had concentrated on ordered magnets and high-Tc superconductors, and we expanded this to disordered quantum magnets.
Unfrustrated systems
The bipartite, 1/5-depleted square lattice of Heisenberg spins is a configuration realised in CaV4O9. Depletion by Ti-doping of the valence-bond units in this structure introduces effectively free S = 1/2 spins with weak, residual interactions. We noticed [1] that the magnitude of these interactions is determined by the impurity separation, but for a bipartite system the sign is determined systematically by the impurity location, and is entirely unfrustrated (the Marshall sign rule). A coherent antiferromagnetic ordering of the entire impurity-spin subsystem results at the lowest temperatures, and may accurately be characterised as a type of ``order by disorder.''
Frustrated systems
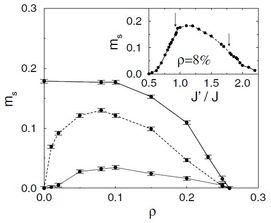
We also pointed out [2] that the frustrated J1-J2 chain is a simple example where, contrary to some received wisdom, nonmagnetic impurites doped into a quantum disordered state do not automatically give rise to free spin degrees of freedom. The double degeneracy of the dimerised ground state means that dimers may be moved with no energy cost at the Majumdar-Ghosh point (J1 = 2J2), screening the impurities without creating free spins. This result may be connected directly to deconfinement of S = 1/2 (spinon) excitations. To the extent that the frustrated, dimerised chain is a good model for CuGeO3, such impurity screening is one explanation for the absence of free spins observed on doping by nonmagnetic impurities in the regime (high dopant density and weak dimerisation) where the frustration is dominant.
S = 1/2 kagome: theory
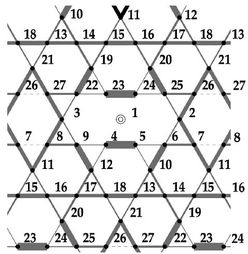
Extending the previous result to two-dimensional systems, we also expected the absence of free-spin formation in cases where the low-energy manifold contains degenerate singlet states. The obvious candidate for an S = 1/2 system with only nearest-neighbour Heisenberg interactions is the kagome lattice, where the lowest levels in the energy spectrum are thought to form a continuum of singlets with a finite triplet gap. We performed a detailed analysis [3] by exact diagonalisation of finite clusters with a single nonmagnetic impurity to find that
- no free spin degrees of freedom arise on doping,
- singlet states are eliminated systematically from below the triplet gap,
- resonating dimers are frozen on triangles with impurities,
- dimer-dimer correlations are of remarkably long range,
- in a magnetic field, local moments are induced over a wide region around each impurity,
- there is evidence for a 1/3 magnetisation plateau and
- doped holes repel each other.
S = 3/2 kagome
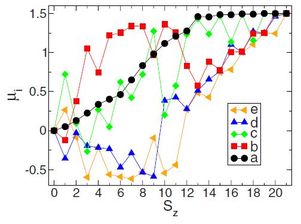
Experimentally, the best results available were for the S = 3/2 system SrCr9pGa12-9pO19 (SCGO). We pushed the same type of studies to S = 3/2 clusters [4] with a view to a more quantitative discussion of SCGO and also Cr-jarosite. Experimentally, our results certainly justified the expectation that a large number of satellite peaks should be expected in NMR measurements due to the intrinsic impurity content (p < 1). Theoretically, although many of the same qualitative features as S = 1/2 remain -- freezing of correlations, no localised moment, long-ranged effects -- unlike S = 1/2 it does not seem that a dimer-based (RVB-type) state can provide a good framework for understanding the S = 3/2 kagome lattice.
S = 1/2 kagome: experiment
The kagome world was turned upside-down in late 2006 by the synthesis of herbertsmithite, ZnCu3(OH)6Cl2, a distorted Cu pyrochlore with Zn on the triangular planes and Cu on the kagome planes. This is not yet a perfect S = 1/2 kagome lattice because of
i) the presence of impurities, in the form of both Zn in the kagome planes, whose effects we know from [3] to be strong, and Cu in the triangular planes, which forms a bond between the kagome lattices;
ii) the presence of Dzyaloshinskii-Moriya interactions on the kagome bonds.
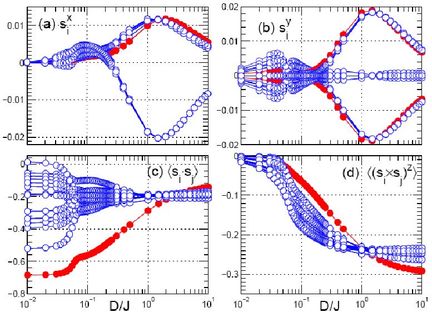
Having preemptively studied the first problem, we considered the second in exact diagonalisation studies of clusters with a single impurity, an out-of-plane DM interaction and an applied magnetic field [5]. We found that a DM interaction D induces an ordered phase beyond D/J = 0.1, and also found the possible presence of a phase intermediate between this and the spin-gapped "true" kagome ground state, which appeared to persist to D/J = 0.06. The effect of spinless impurities in the presence of a DM coupling and a field was again the creation of wide regions of localised moments, now with components oriented both parallel and perpendicular to the applied field.
i) the presence of impurities, in the form of both Zn in the kagome planes, whose effects we know from [3] to be strong, and Cu in the triangular planes, which forms a bond between the kagome lattices;
ii) the presence of Dzyaloshinskii-Moriya interactions on the kagome bonds.
Having preemptively studied the first problem, we considered the second in exact diagonalisation studies of clusters with a single impurity, an out-of-plane DM interaction and an applied magnetic field [5]. We found that a DM interaction D induces an ordered phase beyond D/J = 0.1, and also found the possible presence of a phase intermediate between this and the spin-gapped "true" kagome ground state, which appeared to persist to D/J = 0.06. The effect of spinless impurities in the presence of a DM coupling and a field was again the creation of wide regions of localised moments, now with components oriented both parallel and perpendicular to the applied field.
[1] Order by Disorder from Non-Magnetic Impurities in a Two-Dimensional Quantum Spin Liquid,
S. Wessel, B. Normand, M. Sigrist and S. Haas,
Phys. Rev. Lett 86, 1086 (2001).
[2] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets,
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[3] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[4] Static Impurities in the S = 3/2 Kagome Lattice: Exact Diagonalization Calculations on Small Clusters,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[5] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
S. Wessel, B. Normand, M. Sigrist and S. Haas,
Phys. Rev. Lett 86, 1086 (2001).
[2] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets,
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[3] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[4] Static Impurities in the S = 3/2 Kagome Lattice: Exact Diagonalization Calculations on Small Clusters,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[5] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
