Quantum Phase Transitions
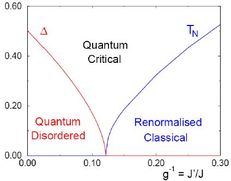
Dimerised quantum magnets have emerged in the last two decades as an ideal class of system for realising particularly clean quantum phase transitions (QPTs). This is a transition between different quantum ground states occurring at zero temperature and controlled by a non-thermal parameter, such as a pressure, doping or magnetic field. The nomenclature is explained in full in the seminal book of this name by Subir Sachdev.
Projects are listed here more or less in chronological order, so please skip down to read the latest news ...
Projects are listed here more or less in chronological order, so please skip down to read the latest news ...
Altering Exchange Interactions

Theoretically, one can always induce a transition by tuning the magnetic coupling constants [1], usually between disordered magnetic phases with a spin gap and ordered, gapless phases. We showed that this is more than a purely academic exercise by using it [2] to place poorly characterised compounds (e.g. those for which single-crystal samples are unavailable) in the relevant magnetic phase diagram. More on these studies can be found under quantum magnetism and frustrated magnetism.. Some materials happen to be located close to an exchange-driven QPT [3], meaning that the energy scales relevant for physical phenomena are far smaller than the scales intrinsic to the system, and in these cases it is possible that (physical or chemical) pressure could indeed drive it through the transition. See quantum magnetism for more.
Field-Induced QPT
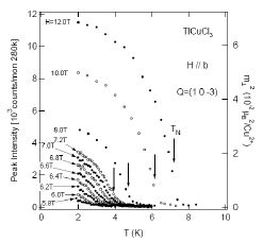
Experimentally, the most transparent approach is to tune the magnetic field, and a number of quantum magnets exist where the excitation gap is small enough to close with a laboratory magnetic field. One is the organometallic, erstwhile spin-ladder system CuHpCl, which we studied both by semiclassical [4] and by microscopic [5] approaches. However, it was the three-dimensionally coupled dimer system TlCuCl3 which drew attention to the field, because i) it has a low critical field of 5.5 T and ii) it appears as large single crystals allowing accurate measurement of the magnetic excitations by inelastic neutron scattering (which has been performed at fields up to 14 T).
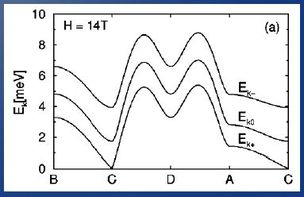
We modelled TlCuCl3 using the bond-operator technique [6,7]. The crucial property of any theoretical approach to the QPT is to use the same framework on both sides of the transition. The bond-operator formalism is naturally adapted to the quantum disordered phase of dimerised spin systems, and we developed it to give a unified, continuous description of the ordered side of the transition by a suitable choice of the ground state. While working on the complete story [7], we also discussed the interaction-tuned QPT and noted the following properties of the excitations.
- For field-induced quantum criticality, there is only one low-lying mode, which at the QPT becomes the sole massless phase mode (Goldstone mode) of the field-ordered magnetic regime. The dispersion at the band minimum remains quadratic at the critical field, with a linear component developing above this field [5-7]. Here the perturbation (the field) commutes with the (Heisenberg) Hamiltonian.
- For coupling-induced quantum criticality, at the QPT one has three massless, linearly dispersive spin waves; on the ordered side one expects only two spin waves (Goldstone modes), and a new type of dynamical excitation in the form of a low-lying but massive longitudinal or amplitude mode of the ordered moment [3,7]. Here the perturbation does not commute with the Hamiltonian, which is why the mode mixed with the condensate is explicitly the one becoming massive.
Magnon Bose-Einstein Condensation
The magnetic field-driven QPT has been described by the notion of Bose-Einstein condensation (BEC) in the lowest-lying magnon mode, which in dimer systems may be represented by hard-core bosons. This description is valid in principle due to the
-- U(1) symmetry,
-- quadratic dispersion and
-- hard-core nature of the bosons (giving them a conserved
number and conjugate chemical potential).
-- U(1) symmetry,
-- quadratic dispersion and
-- hard-core nature of the bosons (giving them a conserved
number and conjugate chemical potential).
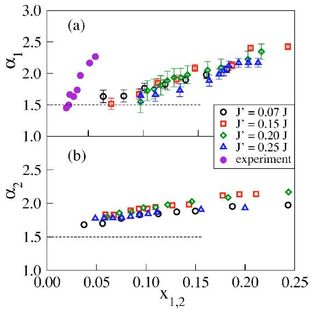
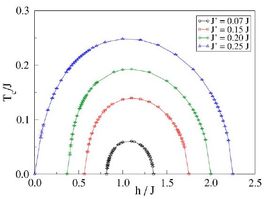
We tested this in practice by using Stochastic Series Expansion QMC simulations [8], currently the most advanced numerical technique available for large spin systems at low temperatures and close to QPTs, at which the spin gap vanishes (and characteristic lengths diverge). We showed that the BEC scenario is applicable, and indeed universal for all systems of the same geometry (i.e. independent of coupling ratio). However, we found systematic deviations from the BEC description away from the transition, indicating that the concept is applicable only at the QPT.
Note, however, that the coupling-induced QPT is not a Bose-Einstein condensation, because the magnon dispersion is linear, not quadratic, at the QPT. While it can certainly be considered as a magnon condensation, it is not in the Bose-Einstein universality class.
Note, however, that the coupling-induced QPT is not a Bose-Einstein condensation, because the magnon dispersion is linear, not quadratic, at the QPT. While it can certainly be considered as a magnon condensation, it is not in the Bose-Einstein universality class.
The Pressure-Induced QPT
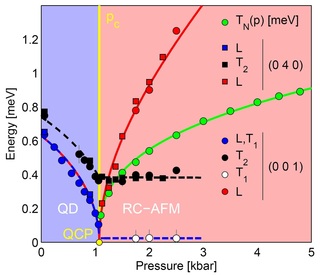
In a major surprise, the pressure-induced phase transition in TlCuCl3 was found to occur at the shockingly low critical pressure of 1.07 kbar -- indicating both a very strong magnetoelastic coupling and a very special system. This led to what is indubitably the best piece of experimental work with which I have ever had the privilege to be associated: inelastic neutron scattering in a He gas pressure cell to map the triplet excitations across the QPT from 0 to 4 kbar. The result [9] was a clear and systematic evolution of the mode gaps which showed
- gap closure on the disordered side,
- a massless spin-wave on the ordered side,
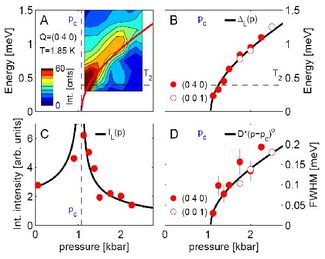
- a uniaxial anisotropy splitting off one mode on the disordered side which becomes a massive spin-wave on the ordered side and
- the clear and unequivocal emergence of the longitudinal mode, its gap growing as the square root of the pressure.
The longitudinal mode is also a "Higgs boson," which has been known in quasi-condensed matter (superconductors, CDWs, quantum magnets, cold atoms) in various guises for a lot longer than it has been in the Standard Model ... Our Higgs boson obviously has a much better lifetime than the one seen at the LHC, and in fact it is by quite a long way the most clearly visible such longitudinal mode known to physics. There are various microscopic reasons for its good visibility in TlCuCl3 [9].
Quantum Criticality
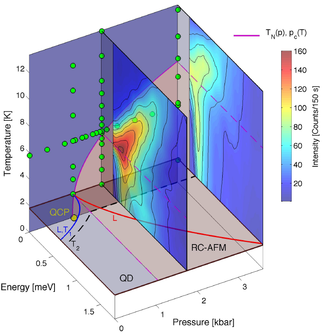
We pushed these studies to finite temperatures to map out the behaviour of the system in the quantum critical regime. Here the dominant energy scale is neither the gap nor TN but the temperature itself. We found [10] that quantum and thermal fluctuations have rather similar effects in destroying long-range order and opening a gap in the excitation spectrum, which is a quite remarkable result ... We also found
- that quantum critical excitations are critically damped (their width scales with their energy),
- that the longitudinal "Higgs" mode of the ordered phase becomes overdamped at finite temperature,
- that a regime of classical criticality appears around the phase transition line, TN(p).
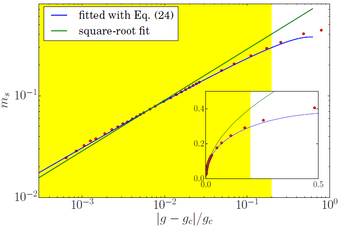
Quantum Critical Scaling
Quantum criticality can be regarded as the interference of quantum and thermal fluctuations, both causing transitions between quantum states In a high-dimensional system there is, heuristically, plenty of phase space and the two do not interfere, leading to mean-field behaviour of all physical quantities as functions of proximity to the QPT. The upper critical dimension marks a crossover to anomalous behaviour, and scaling forms, in a regime where the quantum and thermal processes do compete for the restricted phase space available. At the upper critical dimension itself, the universal scaling behaviour is governed by the mean-field exponents but with logarithmic corrections. A reliable demonstration of the presence of these corrections is a massive numerical challenge that had not been met at the time of the experiments. However, the coupling controlled ("pressure-induced") QPT in three spatial dimensions is at the upper critical dimension and hence we rose to this challenge with the latest algorithms for Stochastic Series Expansion (SSE) quantum Monte Carlo (QMC)
Quantum criticality can be regarded as the interference of quantum and thermal fluctuations, both causing transitions between quantum states In a high-dimensional system there is, heuristically, plenty of phase space and the two do not interfere, leading to mean-field behaviour of all physical quantities as functions of proximity to the QPT. The upper critical dimension marks a crossover to anomalous behaviour, and scaling forms, in a regime where the quantum and thermal processes do compete for the restricted phase space available. At the upper critical dimension itself, the universal scaling behaviour is governed by the mean-field exponents but with logarithmic corrections. A reliable demonstration of the presence of these corrections is a massive numerical challenge that had not been met at the time of the experiments. However, the coupling controlled ("pressure-induced") QPT in three spatial dimensions is at the upper critical dimension and hence we rose to this challenge with the latest algorithms for Stochastic Series Expansion (SSE) quantum Monte Carlo (QMC)
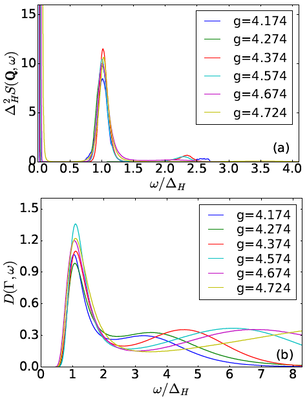
By simulations on systems of sizes up to 2x48x48x48 magnetic sites and temperatures down to 1/96, supplemented by a systematic analysis of the scaling behaviour of a number of static quantities (primarily the order parameter, but also the Néel temperature) we were able to verify the clear presence of logarithmic corrections [11] and also the establish a surprisingly wide quantum critical regime (where this corrected scaling is applicable). To address the scaling of dynamical quantities, particularly the gap and intrinsic width of the amplitude mode, we applied a newly developed improvement of the stochastic analytic continuation (SAC) method for obtaining spectral functions from QMC data. We studied the dynamics through both the spin-spin and dimer-dimer correlation functions [12], again finding the expected logarithmic corrections to scaling and also obtaining results for the width-to-gap ratio that far exceeded the resolution of the experiment. We then also provided an analytical description of both static and dynamic data to unify the two [13].
The Field-Induced QPT at Finite Temperature
When both field and temperature are finite simultaneously, new effects enter which are not present if either is zero. In the theoretical analysis, these are manifest as magnetisation and triplet-correlation terms, and they lead to physical effects causing an observable deviation from field-induced Zeeman splitting. The full theoretical description of the disordered phase in the anisotropic TlCuCl3 system is complete, but the analysis of the experiment is work in progress [14]. On the experimental front, the QPT is clearly of first-order type at finite temperatures, and this reflects the presence of magnetoelastic coupling terms. These are manifestly obvious from the existence of the pressure-induced QPT, but their inclusion in a consistent theory is a major step beyond the current level of sophistication.
The Field-Induced QPT in the Two-Leg Spin Ladder
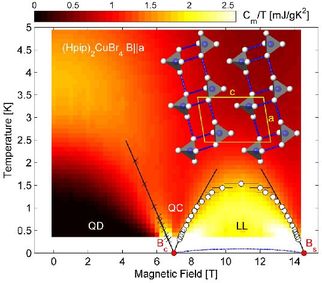
After a number of false hopes, including some of the materials mentioned on these pages, we now have a nearly-perfect spin ladder, the organometallic Cu system (C5H12N)2CuBr4 (bis-piperidinium copper bromide). Because the critical and saturation fields are respectively 7 and 14 T, one may now, without exaggeration, see "everything" there is to see in a spin ladder in this one material. We have done exactly this.
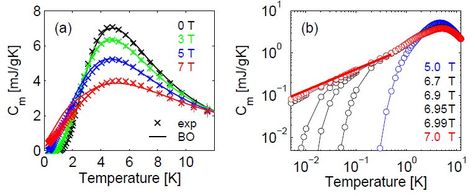
1) By combining a number of approaches, we made a comprehensive study of the thermodynamic response in the gapped, quantum disordered phase up to 7 T and in the gapless, field-induced Luttinger-liquid phase beyond this field, obtaining quantitatively accurate and "parameter-free" fits of data from specific-heat
1) By combining a number of approaches, we made a comprehensive study of the thermodynamic response in the gapped, quantum disordered phase up to 7 T and in the gapless, field-induced Luttinger-liquid phase beyond this field, obtaining quantitatively accurate and "parameter-free" fits of data from specific-heat
and magnetocaloric effect (MCE) measurements [15]. [The parameters are the ladder rung and leg exchange interactions and the g-factor, all extracted separately.]
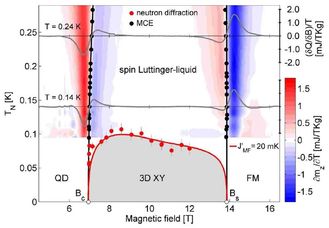
2) There is interladder coupling in any system, and here it leads to a field-induced three-dimensional order below 100 mK. We probed the phase boundary by MCE measurements and the phase itself by magnetic neutron diffraction [16], using our results to calibrate numerical models for weakly coupled quantum systems.
2) There is interladder coupling in any system, and here it leads to a field-induced three-dimensional order below 100 mK. We probed the phase boundary by MCE measurements and the phase itself by magnetic neutron diffraction [16], using our results to calibrate numerical models for weakly coupled quantum systems.
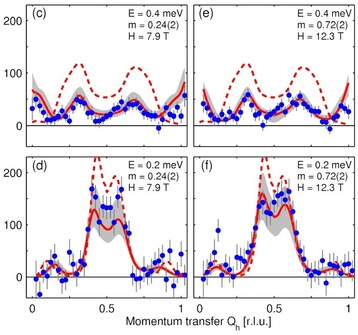
3) The inelastic neutron scattering measurements of the dispersion in supercritical fields are indubitably the second best piece of experimental work with which I have ever had the privilege to be associated. We saw [17] the magnon excitations of the disordered phase split continuously and be replaced by a Faddeev-type spinon continuum above the critical field. This field-induced fractionalisation is accompanied by a continuously tunable incommensuration across the critical (Luttinger-liquid) regime. The experimental results for all momenta, wavevectors and fields were fitted by numerical Bethe Ansatz calculations with one single scale factor for the overall intensity.
4) We have also presented [18] the complete theoretical description of the gapped (quantum disordered and quantum critical) phase in a spin ladder at all fields and temperatures up to the Luttinger-liquid boundary. On taking into account the triplet-correlation and magnetisation terms mentioned above, the results are in quantitative agreement with numerics and experiment even at the phase boundary.
Planar Dimer Systems
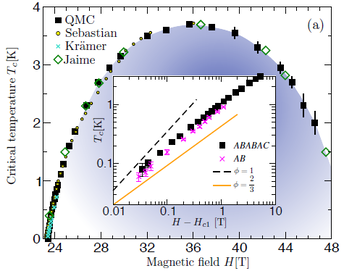
In contrast to the rather straightforward behaviour of coupled ladder systems in a magnetic field, the Cu bilayer material BaCuSi2O6 caused enduring confusion in the field. Because the bilayers have a (1/2,1/2) offset along their stacking axis, antiferromagnetic interbilayer coupling should be perfectly frustrated, and some torque magnetometry data was indeed interpreted as causing a frustration-induced "dimensional reduction" from 3D behavior down to 2D at the field-induced (BEC) QPT at 22.5 T. This was the source of some significant controversy, which we did not help by revealing a structure of 2 or even 3 inequivalent bilayer types [19], as shown on the quantum magnetism page. Subsequent investigation was interpreted as imperfect frustration and a restoration of 3D scaling, but this was turned upside-down by a 2015 study that showed the effective interdimer interactions should be ferromagnetic, and hence there is no interlayer frustration at all. To resolve this situation, we performed inelastic neutron scattering measurements on the most modern time-of-flight sources to verify a structure of 3 bilayers, in an ABABAC stacking sequence, and extract highly accurate interaction parameters [20]; indeed the interdimer and interbilayer interactions were ferromagnetic. We then inserted these parameters into QMC simulations to demonstrate the presence of an additional anomalous scaling regime caused by the difference in energy scales between the inequivalent bilayers. True 3D scaling is obtained only very close to the QPT, while the expected quantum critical regime is actually one of effective anomalous scaling. In combination with a poorly determined critical field, this explains the previous torque magnetometry result. As a follow-up study we found that 10% Sr-doping removed the structural transition that causes bilayer inequivalence, and hence were able to find the true 3D scaling regime originally anticipated for undoped BaCuSi2O6 [21].
In contrast to the rather straightforward behaviour of coupled ladder systems in a magnetic field, the Cu bilayer material BaCuSi2O6 caused enduring confusion in the field. Because the bilayers have a (1/2,1/2) offset along their stacking axis, antiferromagnetic interbilayer coupling should be perfectly frustrated, and some torque magnetometry data was indeed interpreted as causing a frustration-induced "dimensional reduction" from 3D behavior down to 2D at the field-induced (BEC) QPT at 22.5 T. This was the source of some significant controversy, which we did not help by revealing a structure of 2 or even 3 inequivalent bilayer types [19], as shown on the quantum magnetism page. Subsequent investigation was interpreted as imperfect frustration and a restoration of 3D scaling, but this was turned upside-down by a 2015 study that showed the effective interdimer interactions should be ferromagnetic, and hence there is no interlayer frustration at all. To resolve this situation, we performed inelastic neutron scattering measurements on the most modern time-of-flight sources to verify a structure of 3 bilayers, in an ABABAC stacking sequence, and extract highly accurate interaction parameters [20]; indeed the interdimer and interbilayer interactions were ferromagnetic. We then inserted these parameters into QMC simulations to demonstrate the presence of an additional anomalous scaling regime caused by the difference in energy scales between the inequivalent bilayers. True 3D scaling is obtained only very close to the QPT, while the expected quantum critical regime is actually one of effective anomalous scaling. In combination with a poorly determined critical field, this explains the previous torque magnetometry result. As a follow-up study we found that 10% Sr-doping removed the structural transition that causes bilayer inequivalence, and hence were able to find the true 3D scaling regime originally anticipated for undoped BaCuSi2O6 [21].
Other Types of QPT
In separate pieces of work, we have also studied the quantum phase transitions driven by changing the interaction parameter strengths in spin models where ring-exchange interactions [22], staggered magnetic fields [23] and single-ion anisotropy terms [24] compete with the Heisenberg interactions. These are discussed briefly under frustrated magnetism.
QPTs in Electronic Systems
Quantum phase transitions in the presence of charge degrees of freedom are more complex than in spin-only systems. One that we studied for a nanoscopic system was the topological (parity-inversion) transition in the ionic Hubbard model on a flux-threaded nanoring [25], which is reviewed here. We pursued our fascination with topological transitions in the -- admittedly very educational -- ionic Hubbard model to 3- and 4-site versions of the model [26], as reviewed here.
[1] Phase Diagram of the S = 1/2 Frustrated Coupled Ladder System,
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[2] Magnetic Properties of the Coupled Ladder System MgV2O5,
P. Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[3] Dynamical Properties of an Antiferromagnet near the Quantum Critical Point: Application to LaCuO2.5,
B. Normand and T. M. Rice,
Phys. Rev. B 56, 8760 (1997).
[4] Nonlinear sigma-Model Treatment of Quantum Antiferromagnets in a Magnetic Field,
B. Normand, J. Kyriakidis and D. Loss,
Ann. Phys. (Leipzig) 9, 133 (2000).
[5] Quantum Antiferromagnets in a Magnetic Field
B. Normand,
Acta Phys. Polonica B 31, 3005 (2000).
[6] Magnon Dispersion in the Field-Induced Magnetically Ordered Phase of TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. Lett. 89, 077203 (2002).
[7] Pressure- and Field-Induced Magnetic Quantum Phase Transitions in TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. B 69, 054423 (2004).
[8] Universal Scaling at Field-Induced Magnetic Phase Transitions,
O. Nohadani, S. Wessel, B. Normand and S. Haas,
Phys. Rev. B 69, 220402 (2004).
[9] Quantum Magnets under Pressure: Controlling Elementary Excitations in TlCuCl3,
Ch. Rüegg, B. Normand, M. Matsumoto, A. Furrer, D. McMorrow, K. Krämer, H.-U. Güdel,
S. Gvasaliya, H. Mutka and M. Boehm,
Phys. Rev. Lett. 100, 205701 (2008).
[10] Quantum and Classical Criticality in a Dimerized Quantum Antiferromagnet,
P. Merchant, B. Normand, K. W. Krämer, M. Boehm, D. F. McMorrow and Ch. Rüegg,
Nature Physics 10, 373 (2014).
[11] Multiplicative Logarithmic Corrections to Quantum Criticality in Three-Dimensional Dimerized
Antiferromagnets,
Y. Q. Qin, B. Normand, A. W. Sandvik and Z. Y. Meng,
Phys. Rev. B 92, 214401 (2015).
[12] Amplitude (Higgs) Mode in Three-Dimensional Dimerized Antiferromagnets,
Y. Q. Qin, B. Normand, A. W. Sandvik and Z. Y. Meng,
Phys. Rev. Lett. 118, 147207 (2017).
[13] Unifying Static and Dynamic Properties in 3D Quantum Antiferromagnets,
H. D. Scammell, Y. Kharkov, Y. Q. Qin, Z. Y. Meng, B. Normand and O. P. Sushkov,
Phys. Rev. B 96, 174414 (2017).
[14] Magnetic Field–Induced Quantum Critical Excitations and First-Order Classical Phase
Transition in TlCuCl3,
Ch. Rüegg, Ch. Niedermayer, A. Furrer, K. W. Krämer, H.-U. Güdel, H. Mutka and B. Normand,
unpublished.
[15] Thermodynamics of the Spin Luttinger Liquid in a Model Ladder Material,
Ch. Rüegg, K. Kiefer, B. Thielemann, D. F. McMorrow, V. Zapf, B. Normand, M. B. Zvonarev,
P. Bouillot, C. Kollath, T. Giamarchi, S. Capponi, D. Poilblanc, D. Biner and K. W. Krämer,
Phys. Rev. Lett. 101, 247202 (2008).
[16] Field-Controlled Magnetic Order in the Quantum Spin-Ladder System (Hpip)2CuBr4,
B. Thielemann, Ch. Rüegg, K. Kiefer, H. M. Ronnow, B. Normand, P. Bouillot, C. Kollath,
E. Orignac, R. Citro, T. Giamarchi, A. M. Läuchli, D. Biner, K. W. Krämer, F. Wolff-Fabris,
V. Zapf, M. Jaime, J. Stahn, N. B. Christensen, B. Grenier, D. F. McMorrow and J. Mesot,
Phys. Rev. B 79, R020408 (2009).
[17] Direct Observation of Magnon Fractionalization in the Quantum Spin Ladder,
B. Thielemann, Ch. Rüegg, H. M. Ronnow, J.-S. Caux, A. M. Läuchli, B. Normand, D. Biner,
K. W. Krämer, H.-U. Güdel, J. Stahn, S. N. Gvasaliya, K. Habicht, K. Kiefer, M. Boehm,
D. F. McMorrow and J. Mesot,
Phys. Rev. Lett. 102, 107204 (2009).
[18] Complete Bond-Operator Theory of the Two-Chain Spin Ladder,
B. Normand and Ch. Rüegg,
Phys. Rev. B 83, 054415 (2011).
[19] Multiple Magnon Modes and Consequences for the Bose-Einstein Condensed Phase in BaCuSi2O6,
Ch. Rüegg, D. F. McMorrow, B. Normand, H. M. Ronnow, S. E. Sebastian, I. R. Fisher, C. D. Batista, S. Gvasaliya, Ch. Niedermayer and J. Stahn,
Phys. Rev. Lett. 98, 017202 (2007).
[20] Multiple Magnetic Bilayers and Unconventional Criticality without Frustration in BaCuSi2O6,
S. Allenspach, A. Biffin, U. Stuhr, G. S. Tucker, S. Ohira-Kawamura, M. Kofu, D. J. Voneshen,
B. Normand, N. Laflorencie, F. Mila and Ch. Rüegg,
Phys. Rev. Lett. 124, 177205 (2020).
[21] Three-Dimensional Criticality in the Quasi-Two-Dimensional Quantum Magnet Ba0.9Sr0.1CuSi2O6,
S. Allenspach, J. Link, I. Heinmaa, E. Pomjakushina, C. Krellner, J. Lass, G. S. Tucker,
C. Niedermayer, S. Imajo, Y. Kohama, S. Krämer, M. Horvatic, M. Jaime, A. Madsen,
B. Normand, Ch. Rüegg, N. Laflorencie, F. Mila, R. Stern, P. Puphal and F. Weickert,
unpublished.
[22] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[23] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in Staggered
Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[24] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 220402 (2011).
[25] Detection of Topological Transitions by Transport through Molecules and Nanodevices,
A. A. Aligia, K. Hallberg, B. Normand and A. P. Kampf,
Phys. Rev. Lett. 93, 076801 (2004).
[26] Quantum Phase Diagram of the Generalized Ionic Hubbard Model for ABn Chains,
M. E. Torio, A. A. Aligia, G. I. Japaridze and B. Normand,
Phys. Rev. B 73, 115109 (2006).
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[2] Magnetic Properties of the Coupled Ladder System MgV2O5,
P. Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[3] Dynamical Properties of an Antiferromagnet near the Quantum Critical Point: Application to LaCuO2.5,
B. Normand and T. M. Rice,
Phys. Rev. B 56, 8760 (1997).
[4] Nonlinear sigma-Model Treatment of Quantum Antiferromagnets in a Magnetic Field,
B. Normand, J. Kyriakidis and D. Loss,
Ann. Phys. (Leipzig) 9, 133 (2000).
[5] Quantum Antiferromagnets in a Magnetic Field
B. Normand,
Acta Phys. Polonica B 31, 3005 (2000).
[6] Magnon Dispersion in the Field-Induced Magnetically Ordered Phase of TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. Lett. 89, 077203 (2002).
[7] Pressure- and Field-Induced Magnetic Quantum Phase Transitions in TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. B 69, 054423 (2004).
[8] Universal Scaling at Field-Induced Magnetic Phase Transitions,
O. Nohadani, S. Wessel, B. Normand and S. Haas,
Phys. Rev. B 69, 220402 (2004).
[9] Quantum Magnets under Pressure: Controlling Elementary Excitations in TlCuCl3,
Ch. Rüegg, B. Normand, M. Matsumoto, A. Furrer, D. McMorrow, K. Krämer, H.-U. Güdel,
S. Gvasaliya, H. Mutka and M. Boehm,
Phys. Rev. Lett. 100, 205701 (2008).
[10] Quantum and Classical Criticality in a Dimerized Quantum Antiferromagnet,
P. Merchant, B. Normand, K. W. Krämer, M. Boehm, D. F. McMorrow and Ch. Rüegg,
Nature Physics 10, 373 (2014).
[11] Multiplicative Logarithmic Corrections to Quantum Criticality in Three-Dimensional Dimerized
Antiferromagnets,
Y. Q. Qin, B. Normand, A. W. Sandvik and Z. Y. Meng,
Phys. Rev. B 92, 214401 (2015).
[12] Amplitude (Higgs) Mode in Three-Dimensional Dimerized Antiferromagnets,
Y. Q. Qin, B. Normand, A. W. Sandvik and Z. Y. Meng,
Phys. Rev. Lett. 118, 147207 (2017).
[13] Unifying Static and Dynamic Properties in 3D Quantum Antiferromagnets,
H. D. Scammell, Y. Kharkov, Y. Q. Qin, Z. Y. Meng, B. Normand and O. P. Sushkov,
Phys. Rev. B 96, 174414 (2017).
[14] Magnetic Field–Induced Quantum Critical Excitations and First-Order Classical Phase
Transition in TlCuCl3,
Ch. Rüegg, Ch. Niedermayer, A. Furrer, K. W. Krämer, H.-U. Güdel, H. Mutka and B. Normand,
unpublished.
[15] Thermodynamics of the Spin Luttinger Liquid in a Model Ladder Material,
Ch. Rüegg, K. Kiefer, B. Thielemann, D. F. McMorrow, V. Zapf, B. Normand, M. B. Zvonarev,
P. Bouillot, C. Kollath, T. Giamarchi, S. Capponi, D. Poilblanc, D. Biner and K. W. Krämer,
Phys. Rev. Lett. 101, 247202 (2008).
[16] Field-Controlled Magnetic Order in the Quantum Spin-Ladder System (Hpip)2CuBr4,
B. Thielemann, Ch. Rüegg, K. Kiefer, H. M. Ronnow, B. Normand, P. Bouillot, C. Kollath,
E. Orignac, R. Citro, T. Giamarchi, A. M. Läuchli, D. Biner, K. W. Krämer, F. Wolff-Fabris,
V. Zapf, M. Jaime, J. Stahn, N. B. Christensen, B. Grenier, D. F. McMorrow and J. Mesot,
Phys. Rev. B 79, R020408 (2009).
[17] Direct Observation of Magnon Fractionalization in the Quantum Spin Ladder,
B. Thielemann, Ch. Rüegg, H. M. Ronnow, J.-S. Caux, A. M. Läuchli, B. Normand, D. Biner,
K. W. Krämer, H.-U. Güdel, J. Stahn, S. N. Gvasaliya, K. Habicht, K. Kiefer, M. Boehm,
D. F. McMorrow and J. Mesot,
Phys. Rev. Lett. 102, 107204 (2009).
[18] Complete Bond-Operator Theory of the Two-Chain Spin Ladder,
B. Normand and Ch. Rüegg,
Phys. Rev. B 83, 054415 (2011).
[19] Multiple Magnon Modes and Consequences for the Bose-Einstein Condensed Phase in BaCuSi2O6,
Ch. Rüegg, D. F. McMorrow, B. Normand, H. M. Ronnow, S. E. Sebastian, I. R. Fisher, C. D. Batista, S. Gvasaliya, Ch. Niedermayer and J. Stahn,
Phys. Rev. Lett. 98, 017202 (2007).
[20] Multiple Magnetic Bilayers and Unconventional Criticality without Frustration in BaCuSi2O6,
S. Allenspach, A. Biffin, U. Stuhr, G. S. Tucker, S. Ohira-Kawamura, M. Kofu, D. J. Voneshen,
B. Normand, N. Laflorencie, F. Mila and Ch. Rüegg,
Phys. Rev. Lett. 124, 177205 (2020).
[21] Three-Dimensional Criticality in the Quasi-Two-Dimensional Quantum Magnet Ba0.9Sr0.1CuSi2O6,
S. Allenspach, J. Link, I. Heinmaa, E. Pomjakushina, C. Krellner, J. Lass, G. S. Tucker,
C. Niedermayer, S. Imajo, Y. Kohama, S. Krämer, M. Horvatic, M. Jaime, A. Madsen,
B. Normand, Ch. Rüegg, N. Laflorencie, F. Mila, R. Stern, P. Puphal and F. Weickert,
unpublished.
[22] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[23] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in Staggered
Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[24] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 220402 (2011).
[25] Detection of Topological Transitions by Transport through Molecules and Nanodevices,
A. A. Aligia, K. Hallberg, B. Normand and A. P. Kampf,
Phys. Rev. Lett. 93, 076801 (2004).
[26] Quantum Phase Diagram of the Generalized Ionic Hubbard Model for ABn Chains,
M. E. Torio, A. A. Aligia, G. I. Japaridze and B. Normand,
Phys. Rev. B 73, 115109 (2006).
