High-Tc Superconductivity
Projects are listed in chronological order, so please skip down to see what's been going on recently.
Cuprates
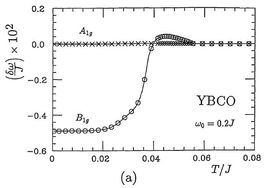
This field needs no introduction or social commentary. I spent my graduate career and first post-doc studying high-temperature superconducting systems within the t-J model, gauging the validity of different treatments of this model by comparison with experimental results. The slave-fermion approach is applicable [1,2] to the properties of lightly doped cuprates. The slave-boson scheme is suitable at higher dopings, including much of the superconducting regime. At the mean-field level it provides a framework in which to understand inelastic neutron scattering and NMR studies of spin excitations, Fermi surfaces measured by photoemission, and -- our unique contribution -- the fact that neutron- and Raman-scattering observations find phonon anomalies not at Tc but at the pseudogap temperature [3-8].
Ladders
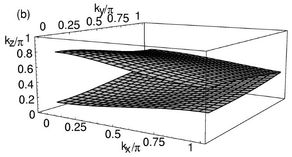
Despite me and all my colleagues being, and remaining, firmly convinced of the need for a strong-coupling (doped Hubbard-model) picture for the cuprates, we did venture to suggest that a spin-fluctuation exchange picture might be appropriate in the doped ladder material LaCuO2.5 [9], where the quasi-one-dimensionality leads to good nesting.
Stripes
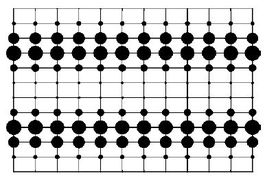
Somewhat later, we investigated the microscopic origin of stripe formation in the known distortions of the ground-state lattice structure of La2-x-yNdySrxCuO4. Static stripes have only ever been observed in compounds with the LTT structure, which breaks the (x,y) symmetry of the basal plane, and we used real-space Hartree-Fock calculations[10] to show that even a weak LTT lattice distortion is sufficient to tip the delicate balance of competing candidate ground states in favour of one-dimensional, charge-inhomogeneous configurations (stripes). This begs the question of why static stripes are not observed in YBa2Cu3O6+x, which has significant (x,y) anisotropy, and we traced this [11] to the much greater next-neighbour (t') kinetic terms in non-LSCO systems. We also compared the relative stability of vertical and diagonal stripes [12], confirming that cuprates should prefer diagonal ones, whence a nearest-neighbour hopping (t) anisotropy is indeed the key physical feature responsible for the observed stripes.
Ring Exchange
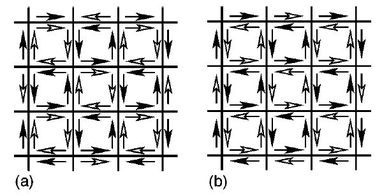
We used the same method to investigate the relation between namely circulating-current states (flux phases) and the cyclic, four-spin (ring-exchange) interaction on the square lattice. These are respectively real and virtual charge or spin currents around the plaquettes. At the Hartree-Fock level, we found that ring-exchange interactions suppress the charge-flux phase (a) on the square lattice but enhance the spin-flux phase (b) where this can be established [13]. By including projected hopping (using Gutzwiller factors), we confirmed i) that the charge-flux phase is a candidate ground state for cuprates, and ii) that the ring-exchange term may determine the magnetic phases close to half-filling (but not the flux phases) [14]. We also made a systematic investigation of ring-exchange interactions, of any magnitude, in one dimension by finding exact solutions in a generalised model on a spin ladder and thus drawing the full phase diagram [15] (see also here).
Iron Superconductors
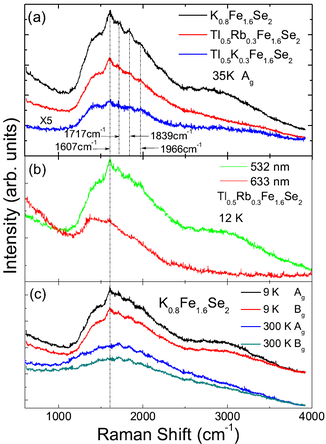
Later I helped my experimental colleagues at Renmin University with the interpretation of their data on the then-new iron superconductor
AyFe2-xSe2 (alkali-intercalated iron selenide, Tc
= 32 K). The Fe superconductors should be good, metallic, intermediate-coupling, spin-fluctuation-exchange systems, but complexities due to the materials and the d-bands of Fe make this difficult to prove. The complexity in this material is that the Fe non-stoichiometry is close to x = 0.4, leading to a 1/5-depleted FeSe layer with, mostly, a strict vacancy ordering stablised by a very strong antiferromagnetic order, with a very large moment, among ferromagnetically coupled four-spin blocks.
i) We used phonon Raman scattering to establish the symmetry of the structure and, in combination with first-principles lattice dynamics, the vacancy ordering pattern [16]. By selective doping studies [17] we showed that Fe-doping alters the higher (FeSe) phonons slowly, implying no dramatic structural changes, while A-doping causes strong changes in the very lowest-lying phonons.
ii) We used two-magnon Raman scattering to show where the optical magnon branches of the 1/5-depleted square lattice lie [18]. There is a highly unconventional drop in the two-magnon intensity exactly at Tc, which is hard to explain except by a microscale cohabitation and strong competition of antiferromagnetism and superconductivity. Whether this cohabitation is a real coexistence or a nanoscale phase separation puzzled a lot of workers in the field for a while
AyFe2-xSe2 (alkali-intercalated iron selenide, Tc
= 32 K). The Fe superconductors should be good, metallic, intermediate-coupling, spin-fluctuation-exchange systems, but complexities due to the materials and the d-bands of Fe make this difficult to prove. The complexity in this material is that the Fe non-stoichiometry is close to x = 0.4, leading to a 1/5-depleted FeSe layer with, mostly, a strict vacancy ordering stablised by a very strong antiferromagnetic order, with a very large moment, among ferromagnetically coupled four-spin blocks.
i) We used phonon Raman scattering to establish the symmetry of the structure and, in combination with first-principles lattice dynamics, the vacancy ordering pattern [16]. By selective doping studies [17] we showed that Fe-doping alters the higher (FeSe) phonons slowly, implying no dramatic structural changes, while A-doping causes strong changes in the very lowest-lying phonons.
ii) We used two-magnon Raman scattering to show where the optical magnon branches of the 1/5-depleted square lattice lie [18]. There is a highly unconventional drop in the two-magnon intensity exactly at Tc, which is hard to explain except by a microscale cohabitation and strong competition of antiferromagnetism and superconductivity. Whether this cohabitation is a real coexistence or a nanoscale phase separation puzzled a lot of workers in the field for a while
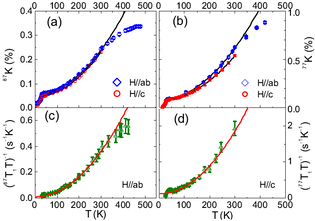
iii) We used NMR to show a clear phase separation, with a nonmagnetic phase which superconducts. The Knight shift and spin-lattice relaxation rate both rise rapidly with temperature above Tc, tracking each other perfectly with a quadratic form [19]. This cannot be a pseudogap, but three-dimensional and very local spin fluctuations, which can be ascribed to the valence bands of Fe. Their contribution is simply additive with a Fermi-liquid contribution, which is due to the conduction electrons and vanishes below Tc. This scenario accounts for the NMR data in all the Fe superconductors away from the SDW transition, which differ only in dimensionality and in dominance of a particular ordering wavevector. There is no need for a complex correlated-electron pseudogap picture as in the cuprates. Later investigation by numerous techniques did confirm that the alkali-intercalated FeSe materials are very much a two-phase system, with nanoscale phase separation of the magnetic and superconducting regions.
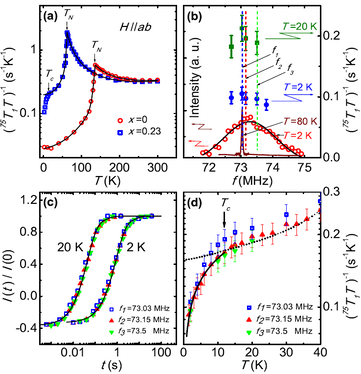
iv) This led us to look elsewhere for microscopic coexistence of antiferromagnetic order and superconductivity in the Fe superconductors. The approach of choice is to study systems with isovalent doping, which results in very slow changes of the electronic properties across the phase diagram. We performed NMR experiments on the iron arsenide Ba(Fe1-xRux)2As2, focussing on an underdoped sample with x = 0.23 which shows a clear antiferromagnetic transition at 60 K and a superconducting one at 15 K [20]. Careful measurements of the Knight shift and spin-lattice relaxation rate established that essentially the entire sample (99.95%) was magnetic below TN and at least 70% of it was superconducting below Tc. The fact that the spin-lattice relaxation rate falls at Tc -- on sites which are already magnetic -- establishes directly that the superconductivity and antiferromagnetism are coexisting on the same Fe ions; this result cannot be the consequence of any type of phase separation. We found a high density of itinerant electrons in the magnetic state of the Ru-doped system, indicating the origin of the superconducting carriers; the lack of obvious competition between the two types of broken symmetry suggests that their carriers occupy different parts of the Fermi surface.
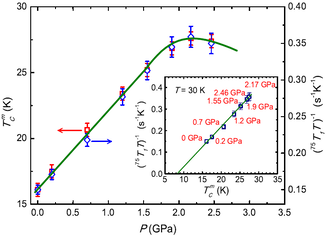
v) This direct connection between superconductivity and magnetism is also manifest in the overdoped material NaFe0.94Co0.06As [21]. Here the low-energy antiferromagnetic spin fluctuations in the normal state, manifest as the Curie-Weiss upturn in the spin-lattice relaxation rate, first increase strongly with pressure but fall again at P > Popt = 2.2 GPa. Neither long-ranged magnetic order nor a structural phase transition, either of which would alter the system behaviour very strongly, occurs up to 2.5 GPa. The superconducting transition temperature, Tc, shows a pressure-dependence identical to the spin fluctuations, this simultaneous optimisation as a function of the electronic structure supporting very strongly a magnetic origin of superconductivity.
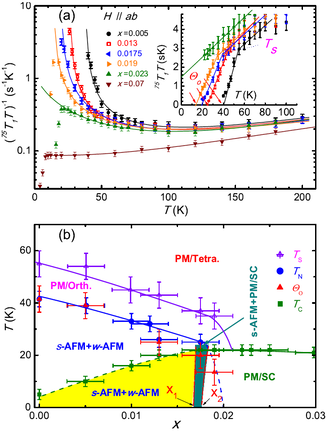
vi) Instead of using pressure as the control parameter we also explored the effect of an applied magnetic field on the phase diagram of NaFe1−xCoxAs [22]. In the underdoped regime (x ≤ 0.017), we found two cohabiting magnetic phases, s-AFM with robust antiferromagnetic (AFM) order and w-AFM with weak and possibly proximity-induced AFM order, whose volume fraction (V ≃ 8%) is approximately constant. Near optimal doping, at x = 0.0175, we observed a phase separation between static antiferromagnetism related to the s-AFM phase and a paramagnetic (PM) phase related to w-AFM. The volume fraction of AFM phase increased upon cooling, but both the Néel temperature and the volume fraction could be suppressed systematically by applying a c-axis magnetic field. On cooling below Tc, superconductivity occupied the PM region and its volume fraction grew at the expense of the AFM phase, demonstrating a phase separation based on volume exclusion. At higher dopings, static antiferromagnetism and even any critical AFM fluctuations were completely suppressed by the superconductivity. Thus the phase diagram we established contains two distinct types of phase separation and reflects a strong competition between AFM and superconducting phases both in real space and in momentum space. We suggested that both this strict mutual exclusion and the robustness of superconductivity against magnetism are consequences of the extreme two-dimensionality of NaFeAs.
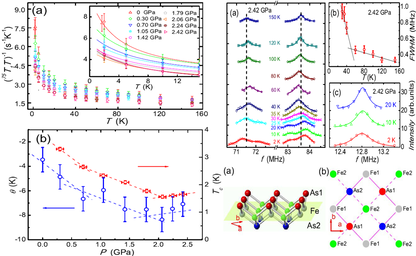
vii) Finally, we also altered the doping state of the FeAs planes to demonstrate that, in a heavily hole-doped iron pnictide superconductor [KFe2As2, Tc ≈ 3.8 K], the low-energy spin fluctuations decrease with applied pressure up to 2 GPa, but then increase again, changing in lockstep with the pressure-induced evolution of Tc. Their diverging nature suggested close proximity to a magnetic quantum critical point at a negative pressure of P ≃ −0.6 GPa. Above 2.2 GPa, the As-NMR satellite spectra split below 40 K, indicating a breaking of As site symmetry and an incipient charge order. These pressure-controlled results demonstrated clearly the presence of nearly critical fluctuations in both the spin and the charge sector [23], which provided essential new input for understanding the origin of superconductivity in iron pnictides.
Mott Insulator
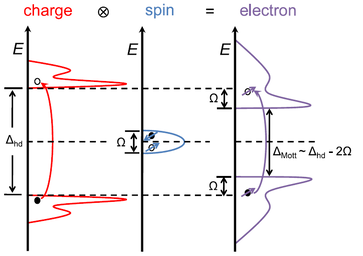
After a break to reassess the situation, we formulated a new approach to describing the Mott insulator: this is the quintessential strongly correlated electronic state and an analytical approximation reproducing its fundamental physics would serve a vital function in developing a full understanding both of the antiferromagnetic insulator and of the Mott state at finite temperatures and dopings. To this end, we introduced a slave-fermion formulation to allow us to study the charge dynamics of the half-filled Hubbard model and applied it on the square lattice. The charge degrees of freedom are represented by fermionic holons and doublons and the Mott-insulating characteristics of the ground state are the consequence of holon-doublon bound-state formation. The bosonic spin degrees of freedom are described by the antiferromagnetic Heisenberg model, yielding long-ranged (Néel) magnetic order at zero temperature. We performed systematic calculations [24] in the self-consistent Born approximation of the average double occupancy, the electronic density of states, the spectral function and the optical conductivity, thereby showing that this method reproduces the lower and upper Hubbard bands, the spectral-weight transfer into a coherent quasiparticle band at their lower edges and the renormalisation of the Mott gap due to the interactions of both quasiparticle species with the magnons. Quantitatively, the square-lattice Hubbard model is one of the best-characterised problems in correlated condensed matter, and benchmarking with many different numerical calculations at zero temperature confirmed the semi-quantitative accuracy of our results for all but the weakest interaction strengths. Thus we could conclude that a self-consistent treatment of the spin-fluctuation effects on the charge degrees of freedom captures all the essential physics of the antiferromagnetic Mott-Hubbard insulator. We then extended this holon-doublon description to finite temperatures [25], again benchmarking its predictions against state-of-the-art quantum Monte Carlo simulations to demonstrate quantitative agreement. Qualitatively, the physical interpretation of our results is that short-ranged spin fluctuations both induce holon-doublon bound states and renormalise the charge sector to form the Hubbard bands. The Mott gap is understood as the charge gap renormalised downward by these spin fluctuations. As the temperature increases, the Mott gap closes before the charge gap, causing a pseudogap regime to appear naturally during the melting of the Mott insulator.
After a break to reassess the situation, we formulated a new approach to describing the Mott insulator: this is the quintessential strongly correlated electronic state and an analytical approximation reproducing its fundamental physics would serve a vital function in developing a full understanding both of the antiferromagnetic insulator and of the Mott state at finite temperatures and dopings. To this end, we introduced a slave-fermion formulation to allow us to study the charge dynamics of the half-filled Hubbard model and applied it on the square lattice. The charge degrees of freedom are represented by fermionic holons and doublons and the Mott-insulating characteristics of the ground state are the consequence of holon-doublon bound-state formation. The bosonic spin degrees of freedom are described by the antiferromagnetic Heisenberg model, yielding long-ranged (Néel) magnetic order at zero temperature. We performed systematic calculations [24] in the self-consistent Born approximation of the average double occupancy, the electronic density of states, the spectral function and the optical conductivity, thereby showing that this method reproduces the lower and upper Hubbard bands, the spectral-weight transfer into a coherent quasiparticle band at their lower edges and the renormalisation of the Mott gap due to the interactions of both quasiparticle species with the magnons. Quantitatively, the square-lattice Hubbard model is one of the best-characterised problems in correlated condensed matter, and benchmarking with many different numerical calculations at zero temperature confirmed the semi-quantitative accuracy of our results for all but the weakest interaction strengths. Thus we could conclude that a self-consistent treatment of the spin-fluctuation effects on the charge degrees of freedom captures all the essential physics of the antiferromagnetic Mott-Hubbard insulator. We then extended this holon-doublon description to finite temperatures [25], again benchmarking its predictions against state-of-the-art quantum Monte Carlo simulations to demonstrate quantitative agreement. Qualitatively, the physical interpretation of our results is that short-ranged spin fluctuations both induce holon-doublon bound states and renormalise the charge sector to form the Hubbard bands. The Mott gap is understood as the charge gap renormalised downward by these spin fluctuations. As the temperature increases, the Mott gap closes before the charge gap, causing a pseudogap regime to appear naturally during the melting of the Mott insulator.
[1] Gauge Theory and Superconductivity in the t'-J Model,
B. Normand, P. A. Lee and N. Nagaosa,
Physica C 185-189, 1479 (1991).
[2] Dynamic Susceptibility and Photoemission in the t-t'-J Model,
B. Normand and P. A. Lee,
Phys. Rev. B 51, 15519 (1995).
[3] Properties of a Mixed-Symmetry Superconductor,
B. Normand, H. Kohno and H. Fukuyama,
Physica C 235-240, 2275 (1994).
[4] Phonons and Spin Excitations in the Extended t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
J. Low Temp. Phys. 99, 531 (1995).
[5] Superconductive Phonon Anomalies in High-Tc Cuprates,
B. Normand, H. Kohno and H. Fukuyama,
J. Phys. Chem. Solids 56, 1739 (1995).
[6] Spin-Phonon Coupling in the Single-Layer Extended t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
Phys. Rev. B 53, 856 (1996).
[7] Dynamic Susceptibility and Phonon Anomalies in the Bilayer t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
J. Phys. Soc. Jpn. 64, 3903 (1995).
[8] \pi-Excitation and Resonant Neutron Scattering: a Mean-Field Study,,
H. Kohno, B. Normand and H. Fukuyama,
Physica C 282-287, 1685 (1997).
[9] Possible Superconductivity in the doped Ladder Compound La1-xSrxCuO2.5,
B. Normand, D. F. Agterberg and T. M. Rice,
Phys. Rev. Lett 82, 4296 (1999).
[10] Microscopic Origin of Static Stripes in Cuprates,
B. Normand and A. P. Kampf,
Phys. Rev. B 64, 024521 (2001).
[11] Suppression of Static Stripe Formation by Next-Neighbor Hopping,
B. Normand and A. P. Kampf,
Phys. Rev. B 65, 020509 (2002).
[12] Vertical and Diagonal Stripes in the Extended Hubbard Model,
M. Raczkowski, B. Normand and A. M. Oleś,
Phys. Stat. Sol. (b) 236, 376 (2003).
[13] Circulating-Current States and Ring-Exchange Interactions in Cuprates,
B. Normand and A. M. Oleś,
Physica C 408-410, 252 (2004).
[14] Circulating-Current States and Ring-Exchange Interactions in Cuprates,
B. Normand and A. M. Oleś,
Phys. Rev. B 70, 134407 (2004).
[15] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[16] Vacancy Ordering and Phonon Spectrum in the Fe Superconductor K0.8Fe1.6Se2,
A. M. Zhang, K. Liu, J. H. Xiao, J. B. He, D. M. Wang, G. F. Chen, B. Normand and Q. M. Zhang,
Phys. Rev. B 85, 024518 (2012).
[17] Effect of Iron Content and Potassium Substitution in A0.8Fe1.6Se2 (A = K, Rb, Tl) Superconductors:
a Raman-Scattering Investigation,
A. M. Zhang, K. Liu, J. H. Xiao, J. B. He, D. M. Wang, G. F. Chen, B. Normand and Q. M. Zhang,
Phys. Rev. B 86, 134502 (2012).
[18] Two-magnon Raman-scattering in A0.8Fe1.6Se2 systems (A = K, Cs, Rb, and Tl): competition
between superconductivity and antiferromagnetic order,
A. M. Zhang, J. H. Xiao, Y. S. Li, J. B. He, D. M. Wang, G. F. Chen, B. Normand, Q. M. Zhang
and T. Xiang,
Phys. Rev. B 85, 214508 (2012).
[19] Local spin fluctuations in iron-based superconductors: 77Se and 87Rb NMR measurements
on Tl0.47Rb0.34Fe1.63Se2,
L. Ma, G. F. Ji, J. Dai, J. B. He, D. M. Wang, G. F. Chen, B. Normand and W. Q. Yu,
Phys. Rev. B 84, 220505(R) (2012).
[20] Microscopic Coexistence of Superconductivity and Antiferromagnetic Order in Underdoped
Ba(Fe1-xRux)2As2,
L. Ma, G. F. Ji, J. Dai, X. R. Lu, M. J. Eom, J. S. Kim, B. Normand and W. Q. Yu,
Phys. Rev. Lett. 109, 197002 (2012).
[21] Simultaneous Optimization of Spin Fluctuations and Superconductivity under Pressure in an
Iron-based Superconductor,
G. F. Ji, J. S. Zhang, L. Ma, P. Fan, P. S. Wang, J. Dai, G. T. Tan, Y. Song, C. L. Zhang, P. C. Dai,
B. Normand and W. Q. Yu,
Phys. Rev. Lett. 111, 107004 (2013).
[22] Phase Separation, Competition and Volume Fraction Control in NaFe1−xCoxAs,
L. Ma, J. Dai, X. R. Lu, P. S. Wang, Y. Song, D. Hu, S. L. Li, P. C. Dai, C. L. Zhang,
B. Normand and W. Q. Yu,
Phys. Rev. B 90, 144502 (2014).
[23] Nearly-Critical Spin and Charge Fluctuations in KFe2As2 Observed by High-Pressure NMR,
P. S. Wang, P. Zhou, J. Dai, J. Zhang, X. X. Ding, H. Lin, H. H. Wen, B. Normand, R. Yu
and W. Q. Yu,
Phys. Rev. B 93, 085129 (2016).
[24] Charge Dynamics of the Antiferromagnetically Ordered Mott Insulator,
X. J. Han, Y. Liu, Z. Y. Liu, X. Li, J. Chen, Z. Y. Xie, B. Normand and T. Xiang,
New. J. Phys. 18, 103004 (2016).
[25] Finite-Temperature Charge Dynamics and the Melting of the Mott Insulator,
X. J. Han, C. Chen, J. Chen, H. D. Xie, R. Z. Huang, H. J. Liao, B. Normand, Z. Y. Meng
and T. Xiang,
Phys. Rev. B 99, 245150 (2019).
B. Normand, P. A. Lee and N. Nagaosa,
Physica C 185-189, 1479 (1991).
[2] Dynamic Susceptibility and Photoemission in the t-t'-J Model,
B. Normand and P. A. Lee,
Phys. Rev. B 51, 15519 (1995).
[3] Properties of a Mixed-Symmetry Superconductor,
B. Normand, H. Kohno and H. Fukuyama,
Physica C 235-240, 2275 (1994).
[4] Phonons and Spin Excitations in the Extended t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
J. Low Temp. Phys. 99, 531 (1995).
[5] Superconductive Phonon Anomalies in High-Tc Cuprates,
B. Normand, H. Kohno and H. Fukuyama,
J. Phys. Chem. Solids 56, 1739 (1995).
[6] Spin-Phonon Coupling in the Single-Layer Extended t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
Phys. Rev. B 53, 856 (1996).
[7] Dynamic Susceptibility and Phonon Anomalies in the Bilayer t-J Model,
B. Normand, H. Kohno and H. Fukuyama,
J. Phys. Soc. Jpn. 64, 3903 (1995).
[8] \pi-Excitation and Resonant Neutron Scattering: a Mean-Field Study,,
H. Kohno, B. Normand and H. Fukuyama,
Physica C 282-287, 1685 (1997).
[9] Possible Superconductivity in the doped Ladder Compound La1-xSrxCuO2.5,
B. Normand, D. F. Agterberg and T. M. Rice,
Phys. Rev. Lett 82, 4296 (1999).
[10] Microscopic Origin of Static Stripes in Cuprates,
B. Normand and A. P. Kampf,
Phys. Rev. B 64, 024521 (2001).
[11] Suppression of Static Stripe Formation by Next-Neighbor Hopping,
B. Normand and A. P. Kampf,
Phys. Rev. B 65, 020509 (2002).
[12] Vertical and Diagonal Stripes in the Extended Hubbard Model,
M. Raczkowski, B. Normand and A. M. Oleś,
Phys. Stat. Sol. (b) 236, 376 (2003).
[13] Circulating-Current States and Ring-Exchange Interactions in Cuprates,
B. Normand and A. M. Oleś,
Physica C 408-410, 252 (2004).
[14] Circulating-Current States and Ring-Exchange Interactions in Cuprates,
B. Normand and A. M. Oleś,
Phys. Rev. B 70, 134407 (2004).
[15] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[16] Vacancy Ordering and Phonon Spectrum in the Fe Superconductor K0.8Fe1.6Se2,
A. M. Zhang, K. Liu, J. H. Xiao, J. B. He, D. M. Wang, G. F. Chen, B. Normand and Q. M. Zhang,
Phys. Rev. B 85, 024518 (2012).
[17] Effect of Iron Content and Potassium Substitution in A0.8Fe1.6Se2 (A = K, Rb, Tl) Superconductors:
a Raman-Scattering Investigation,
A. M. Zhang, K. Liu, J. H. Xiao, J. B. He, D. M. Wang, G. F. Chen, B. Normand and Q. M. Zhang,
Phys. Rev. B 86, 134502 (2012).
[18] Two-magnon Raman-scattering in A0.8Fe1.6Se2 systems (A = K, Cs, Rb, and Tl): competition
between superconductivity and antiferromagnetic order,
A. M. Zhang, J. H. Xiao, Y. S. Li, J. B. He, D. M. Wang, G. F. Chen, B. Normand, Q. M. Zhang
and T. Xiang,
Phys. Rev. B 85, 214508 (2012).
[19] Local spin fluctuations in iron-based superconductors: 77Se and 87Rb NMR measurements
on Tl0.47Rb0.34Fe1.63Se2,
L. Ma, G. F. Ji, J. Dai, J. B. He, D. M. Wang, G. F. Chen, B. Normand and W. Q. Yu,
Phys. Rev. B 84, 220505(R) (2012).
[20] Microscopic Coexistence of Superconductivity and Antiferromagnetic Order in Underdoped
Ba(Fe1-xRux)2As2,
L. Ma, G. F. Ji, J. Dai, X. R. Lu, M. J. Eom, J. S. Kim, B. Normand and W. Q. Yu,
Phys. Rev. Lett. 109, 197002 (2012).
[21] Simultaneous Optimization of Spin Fluctuations and Superconductivity under Pressure in an
Iron-based Superconductor,
G. F. Ji, J. S. Zhang, L. Ma, P. Fan, P. S. Wang, J. Dai, G. T. Tan, Y. Song, C. L. Zhang, P. C. Dai,
B. Normand and W. Q. Yu,
Phys. Rev. Lett. 111, 107004 (2013).
[22] Phase Separation, Competition and Volume Fraction Control in NaFe1−xCoxAs,
L. Ma, J. Dai, X. R. Lu, P. S. Wang, Y. Song, D. Hu, S. L. Li, P. C. Dai, C. L. Zhang,
B. Normand and W. Q. Yu,
Phys. Rev. B 90, 144502 (2014).
[23] Nearly-Critical Spin and Charge Fluctuations in KFe2As2 Observed by High-Pressure NMR,
P. S. Wang, P. Zhou, J. Dai, J. Zhang, X. X. Ding, H. Lin, H. H. Wen, B. Normand, R. Yu
and W. Q. Yu,
Phys. Rev. B 93, 085129 (2016).
[24] Charge Dynamics of the Antiferromagnetically Ordered Mott Insulator,
X. J. Han, Y. Liu, Z. Y. Liu, X. Li, J. Chen, Z. Y. Xie, B. Normand and T. Xiang,
New. J. Phys. 18, 103004 (2016).
[25] Finite-Temperature Charge Dynamics and the Melting of the Mott Insulator,
X. J. Han, C. Chen, J. Chen, H. D. Xie, R. Z. Huang, H. J. Liao, B. Normand, Z. Y. Meng
and T. Xiang,
Phys. Rev. B 99, 245150 (2019).
