Quantum Magnetism
A quantum magnet is a spin system with sufficiently small effective dimensionality d and ionic spin S that quantum mechanical fluctuations dominate its behaviour. The field of study has grown enormously since the advent of high-Tc superconductivity, due in unequal part to some theoretical impetus and some very talented experimental physicists and synthetic chemists. Most of my research is connected in some way to quantum magnetism, and so in addition to a few projects that defy further classification, this page is largely an overview with pointers to the other pages.
Projects are listed roughly in chronological order, so please skip down to see the new stuff ...
Projects are listed roughly in chronological order, so please skip down to see the new stuff ...
Spin Ladders
In the early days of spin ladders (systems with small numbers of strongly coupled spin chains) we focussed on interladder coupling, which is unavoidable in real materials. LaCuO2.5 [1] is a ladder material with unfrustrated interladder coupling, and turned out to be located close to the quantum phase transition (QPT) from quantum disordered to classically ordered magnetism. We looked [2] at the continuous evolution of physical properties through the QPT, and particularly at a novel dynamical excitation expected near the QPT on the ordered side -- a longitudinal mode, or amplitude fluctuation of the ordered moment (which is small and malleable in this regime). Many years later, this mode was measured experimentally as a function of applied pressure in the theorist's dream material, TlCuCl3. More about this can be found on the quantum phase transitions page. Back at the time, and driven by the unavoidable experimental situation that single crystals of LaCuO2.5 can be prepared only with 14% Sr doping, we speculated instead [3] on possible superconductivity in doped, coupled spin ladders.
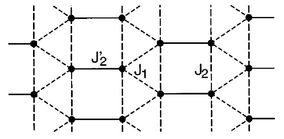
Another important interladder coupling configuration is the frustrated "trellis lattice" structure of the cuprate SrCu2O3 and the vanadates XV2O5 (X = Ca and Mg). We looked at this [4] for general couplings, finding a rich variety of ground-state types due to the frustrated coupling, and were able [5] to place MgV2O5 very close to one of the QPT boundaries in the phase diagram. At the same time we thought [6] that frustrated coupling might be the key to the curious properties of (VO)2P2O7 (VOPO), but improved crystal quality and additional experiments led us later to show [7] that a two-plane magnetic unit cell and strong magnetoelastic coupling were the ingredients required for a consistent explanation.
Spin-Dimer Systems
The synthesis of some organometallic, ladder-like compounds showing spin-gap and quantum critical phenomena on the energy scale of experimentally accessible magnetic fields also led us [8,9] to the problem of the field-induced QPT. However, it was the material TlCuCl3, a three-dimensionally coupled, small-gap dimer system (Hc = 5.5 T) that grows as high-quality, neutron-scattering-sized single crystals, which opened the floodgates for high-quality static and dynamic data. All our studies of the ground state and in particular the dynamical excitations, at both the field-induced [10,11] and pressure-induced [11,12] quantum critical points, are summarised on the quantum phase transitions page.
Hard-Core Bosons at Finite Temperatures
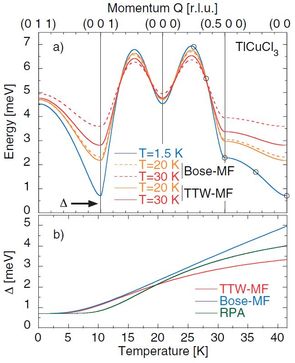
The triplet excitations in a dimer spin system are bosonic, but obey an exclusion constraint at every dimer site. This hard-core boson nature is the foundation for the Bose-Einstein condensation scenario as a description of the field-induced ordered phase, which we tested by quantum Monte Carlo simulations. We found it to be valid, and (on consistent treatment of the data) surprisingly universal, at the QPT, but not appropriate away from this point [13]. Again, further details are on the quantum phase transitions page.
The hard-core-boson nature also leads to a new phenomenon in the mode dispersion relations at finite temperatures. The thermal occupation of magnon modes means that a test magnon trying to propagate through the lattice is blocked due to the exclusion constraint. Thus, without changing the exchange
The hard-core-boson nature also leads to a new phenomenon in the mode dispersion relations at finite temperatures. The thermal occupation of magnon modes means that a test magnon trying to propagate through the lattice is blocked due to the exclusion constraint. Thus, without changing the exchange
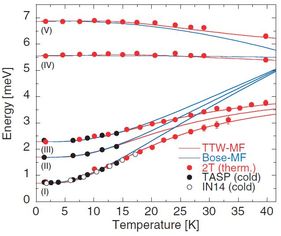
constants, the magnon bands are narrowed significantly -- a strong change in energy with temperature not accompanied simply by a thermal smearing of the mode. For the consistent treatment of finite-temperature data, we followed [14] the TTW Ansatz, a global statistical reweighting of the free-boson partition function to account for the local exclusion, to deduce an effective magnon occupation function. This resulted in spectacularly good agreement with the measured thermal renormalisation of the full magnon dispersion in TlCuCl3.
Planar Dimer Systems
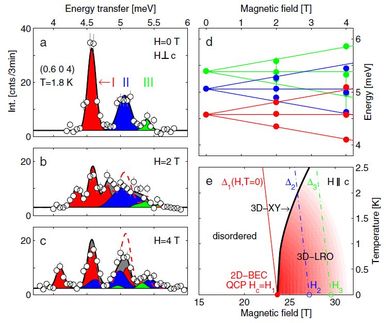
Another spin dimer material to cause a fair amount of experimental and theoretical excitement was BaCuSi2O6, a bilayer system creating planar dimer sheets with frustrated interplane coupling. By inelastic neutron scattering measurements of the magnon dispersion, we found [15] that successive planes were not structurally equivalent, thereby altering the understanding of the effective system dimensionality, the field-induced (BEC) QPT, the interlayer frustration and the possible role of the lattice. Many years and a lot of lingering confusion later, we resolved the issue of the anomalous scaling at the QPT [16], as detailed on the quantum phase transitions page.
The Spin Ladder Revisited: (Hpip)2CuBr4
The nearly-perfect spin ladder material has now been found, and its name is bis-piperidinium copper bromide. We provided the theoretical backing for a number of very elegant experimental measurements of thermodynamics across the entire (H,T) phase diagram [17], of the field-induced three-dimensionally ordered phase at T < 100 mK [18] and of the field-induced fractionalisation of magnons into the spinon excitations chancteristic of the intermediate-field Luttinger-liquid regime [19]. We also demonstrated [20] that the bond-operator framework can provide a complete description of the gapped quantum phases of a two-leg spin ladder. More details about all of this can be found on the quantum phase transitions page. Some time later, when single crystals of the Cl analogue became available, we were able to investigate the high-field phase in detail [21]. In fact here we also used the favourable system parameters to find the two-triplet bound state at zero field [21]; this is an excitation that is not contained in the regular bond-operator description and needs a more advanced treatment (which we provided) to describe it.
More Planar Quantum Magnets
We used the extremely well characterised cuprate parent material La2CuO4 to address a problem ubiquitous in quantum magnetism: the effects of thermal fluctuations. Specifically, we measured the distribution of positions of Cu and O atoms at 2 K and at 300 K [22], finding that the root-mean-square deviation is doubled; in other words, zero-point atomic motion is quantitatively the same as the effect of room temperature. We went on to investigate isotope effects, and to estimate the consequences of these positional fluctations for the hopping and superexchange energies in the cuprate plane, finding rather broad distributions, but little change in average values.
We used the extremely well characterised cuprate parent material La2CuO4 to address a problem ubiquitous in quantum magnetism: the effects of thermal fluctuations. Specifically, we measured the distribution of positions of Cu and O atoms at 2 K and at 300 K [22], finding that the root-mean-square deviation is doubled; in other words, zero-point atomic motion is quantitatively the same as the effect of room temperature. We went on to investigate isotope effects, and to estimate the consequences of these positional fluctations for the hopping and superexchange energies in the cuprate plane, finding rather broad distributions, but little change in average values.
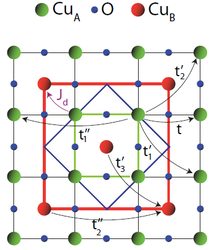
Another study adding extra dimensions to our knowledge of planar cuprates concerned the "half-stuffed" material Ba2Cu3O4Cl2, in which half of the plaquettes in the lattice contain an extra Cu ion at their centre. Because of the disparity in hopping integrals between the linear geometry of the plaquette edges and the near-perpendicular geometry of Cu-O-Cu bonds linking to the centre sites, the latter form a rather separate magnetic subsystem [23]. Finally, the metal-organic material [(CuF2(H2O)2)2pyrazine].is planar only until one applies enough pressure: the magnetic interaction parameters show a gigantic pressure-induced alteration, and then a dimensionality-switching phase transition occurs at which it turns into a system of spin chains [24].
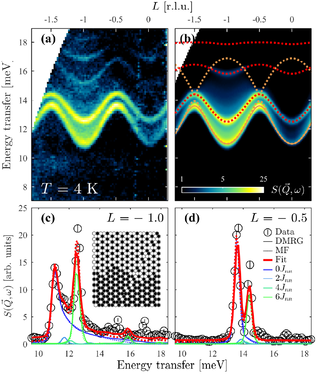
More Quantum Spin Chains
The Ising chain is one of the oldest problems in the book of quantum magnetism, and provides a very simple example of fractional excitations, variously known as domain walls, kinks and solitons. Ising chains in a confining field, established by all of the neighbouring chains in a 3D solid, hit the headlines in the context of the E8 symmetry group of Zeeman-ladder states in CoNb2O6. We studied a material hosting Ising chains in a triangular array, which leads to a frustrated situation with two low-temperature phase transitions setting different and inequivalent staggered fields. Because some of the chains have zero net field, we were able to observe the continuum response of the isolated Ising chain coexisting with several different types of Zeeman-ladder state [25]. Increasing temperature leads to systematic changes in the chain environments, and we provided some quantitative numerical modelling to account for all of the observed dynamics.
The Ising chain is one of the oldest problems in the book of quantum magnetism, and provides a very simple example of fractional excitations, variously known as domain walls, kinks and solitons. Ising chains in a confining field, established by all of the neighbouring chains in a 3D solid, hit the headlines in the context of the E8 symmetry group of Zeeman-ladder states in CoNb2O6. We studied a material hosting Ising chains in a triangular array, which leads to a frustrated situation with two low-temperature phase transitions setting different and inequivalent staggered fields. Because some of the chains have zero net field, we were able to observe the continuum response of the isolated Ising chain coexisting with several different types of Zeeman-ladder state [25]. Increasing temperature leads to systematic changes in the chain environments, and we provided some quantitative numerical modelling to account for all of the observed dynamics.

Normally all our favourite quantum magnets are well described within a single framework: this one has magnetic order and spin-wave excitations (magnons), that one is dimerised and shows gapped, triplet excitations, another is gapless and disordered with fractional, spinonic excitations. Thus it was something of a surprise when we looked at SeCuO3 and found all three types of excitation coexisting in the same material [26]. The Cu ions form two subsystems, one of strong dimer pairs which host the triplons and one of weakly coupled spin chains. This coupling spans all three dimensions and is sufficient to allow weak magnetic order, on which gapped spin waves may propagate. However, directly above the spin-wave branch is a regime of continuum scattering, indicating that the spin excitations are deconfining into spinon pairs. The 3D network has significant frustration and the continua are far from being quasi-1D, so the exact nature of deconfinement in this system remains to be elucidated.
Doping with Nonmagnetic Impurities
Doping quantum-disordered magnets with nonmagnetic impurities leads to some fascinating phenomena in unfrustrated [27] and frustrated [28-31] systems, many of which can be detected by local measurements (NMR and muon spin resonance). It can also be a very dirty and abrupt way of creating a quantum phase transition, although I have never been more than tangentially involved with this type of study. This topic has its own separate page.
Frustrated Quantum Magnetism
I have spent a lot of time and effort looking for high-dimensional spinons and spin liquids in highly frustrated models for quantum magnets. Specifically, we looked for spinons in the Heisenberg model on the kagome lattices [29] and in Klein models on checkerboard and pyrochlore lattices [32-34], and for spin liquids in orbitally degenerate models on the triangular lattice [35,36]. I also wrote a review article [37] on frustrated quantum magnetism, which I later helped to make redundant by further work to resolve the true ground state of the kagome Heisenberg antiferromagnet [38-41]. This topic also has its own separate page, which in turn feeds to further subsequent lines of research.
The Rich Variety of Quantum Magnetism
In a number of independent projects, we have worked on spin ladders with cyclic ring exchange [42], on coupled-chain systems in staggered magnetic fields [43], and on the Gaussian transition in S = 1 chains with single-ion anisotropy [44]. The review of these projects can be found under frustrated magnetism.
Nanoscopic Magnetism
My projects on quantum nanomagnets [45-48] can be found on their own page. Also reviewed there is our use of flux-threaded nanorings to investigate the interaction and separation [49] of spin and charge degrees of freedom in models of interacting electrons, and their combination in topological phase transitions [50].
Quantum Magnets with Charge Degrees of Freedom
Electronic charge makes everything much more complex, both in experiment and in theory. However, it is also where all the most important phenomena are to be found ... In addition to the work on nanorings [49,50], our efforts to include and understand the effects of charge degrees of freedom in quantum magnetic systems also encompassed the generalised ionic Hubbard model [51], reviewed here.
[1] Electronic and Magnetic Properties of LaCuO2.5,
B. Normand and T. M. Rice,
Phys. Rev. B 54, 7180 (1996).
[2] Dynamical Properties of an Antiferromagnet near the Quantum Critical Point: Application to LaCuO2.5,
B. Normand and T. M. Rice,
Phys. Rev. B 56, 8760 (1997).
[3] Possible Superconductivity in the doped Ladder Compound La1-xSrxCuO2.5,
B. Normand, D. F. Agterberg and T. M. Rice,
Phys. Rev. Lett 82, 4296 (1999).
[4] Phase Diagram of the S = 1/2 Frustrated Coupled Ladder System,
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[5] Magnetic Properties of the Coupled Ladder System MgV2O5,
P.Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[6] Magnetic Properties of (VO)2P2O7 from Frustrated Interchain Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 58, R14705 (1998).
[7] Magnetic Properties of (VO)2P2O7: Two-Plane Structure and Spin-Phonon Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 63, 134418 (2001).
[8] Nonlinear sigma Model Treatment of Quantum Antiferromagnets in a Magnetic Field,
B. Normand, J. Kyriakidis and D. Loss,
Ann. Phys. (Leipzig) 9, 133 (2000).
[9] Quantum Antiferromagnets in a Magnetic Field,
B. Normand,
Acta Phys. Polonica B 31, 3005 (2000).
[10] Magnon Dispersion in the Field-Induced Magnetically Ordered Phase of TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. Lett. 89, 077203 (2002).
[11] Pressure- and Field-Induced Magnetic Quantum Phase Transitions in TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. B 69, 054423 (2004).
[12] Quantum Magnets under Pressure: Controlling Elementary Excitations in TlCuCl3,
Ch. Rüegg, B. Normand, M. Matsumoto, A. Furrer, D. McMorrow, K. Krämer, H.-U. Güdel,
S. Gvasaliya, H. Mutka and M. Boehm,
Phys. Rev. Lett. 100, 205701 (2008).
[13] Universal Scaling at Field-Induced Magnetic Phase Transitions,
O. Nohadani, S. Wessel, B. Normand and S. Haas,
Phys. Rev. B 69, 220402 (2004).
[14] Quantum Statistics of Interacting Dimer Spin Systems,
Ch. Rüegg, B. Normand, M. Matsumoto, Ch. Niedermayer, A. Furrer, K. W. Krämer, H.-U. Güdel,
Ph. Bourges, Y. Sidis and H. Mutka,
Phys. Rev. Lett. 95, 267201 (2005).
[15] Multiple Magnon Modes and Consequences for the Bose-Einstein Condensed Phase in BaCuSi2O6,
Ch. Rüegg, D. F. McMorrow, B. Normand, H. M. Ronnow, S. E. Sebastian, I. R. Fisher, C. D. Batista, S. Gvasaliya, Ch. Niedermayer and J. Stahn,
Phys. Rev. Lett. 98, 017202 (2007).
[16] Multiple Magnetic Bilayers and Unconventional Criticality without Frustration in BaCuSi2O6,
S. Allenspach, A. Biffin, U. Stuhr, G. S. Tucker, S. Ohira-Kawamura, M. Kofu, D. J. Voneshen,
B. Normand, N. Laflorencie, F. Mila and Ch. Rüegg,
Phys. Rev. Lett. 124, 177205 (2020).
[17] Thermodynamics of the Spin Luttinger Liquid in a Model Ladder Material,
Ch. Rüegg, K. Kiefer, B. Thielemann, D. F. McMorrow, V. Zapf, B. Normand, M. B. Zvonarev,
P. Bouillot, C. Kollath, T. Giamarchi, S. Capponi, D. Poilblanc, D. Biner and K. W. Krämer,
Phys. Rev. Lett. 101, 247202 (2008).
[18] Field-Controlled Magnetic Order in the Quantum Spin-Ladder System (Hpip)2CuBr4,
B. Thielemann, Ch. Rüegg, K. Kiefer, H. M. Ronnow, B. Normand, P. Bouillot, C. Kollath,
E. Orignac, R. Citro, T. Giamarchi, A. M. Läuchli, D. Biner, K. W. Krämer, F. Wolff-Fabris,
V. Zapf, M. Jaime, J. Stahn, N. B. Christensen, B. Grenier, D. F. McMorrow and J. Mesot,
Phys. Rev. B 79, R020408 (2009).
[19] Direct Observation of Magnon Fractionalization in the Quantum Spin Ladder,
B. Thielemann, Ch. Rüegg, H. M. Ronnow, J.-S. Caux, A. M. Läuchli, B. Normand, D. Biner,
K. W. Krämer, H.-U. Güdel, J. Stahn, S. N. Gvasaliya, K. Habicht, K. Kiefer, M. Boehm,
D. F. McMorrow and J. Mesot,
Phys. Rev. Lett. 102, 107204 (2009).
[20] Complete Bond-Operator Theory of the Two-Chain Spin Ladder,
B. Normand and Ch. Rüegg,
Phys. Rev. B 83, 054415 (2011).
[21] Bound States and Field-Polarized Haldane Modes in a Quantum Spin Ladder,
S. Ward, M. Mena, P. Bouillot, C. Kollath, T. Giamarchi, K. P. Schmidt, B. Normand, K. W. Krämer,
D. Biner, R. Bewley, T. Guidi, M. Boehm, D. F. McMorrow and Ch. Rüegg,
Phys. Rev. Lett. 118, 177202 (2017).
[22] Quantum and Thermal Ionic motion, Oxygen Isotope Effect, and Superexchange Distribution
in La2CuO4,
P. S. Häfliger, S. Gerber, R. Pramod, V. I. Schnells, B. dalla Piazza, R. Chati, V. Pomjakushin,
K. Conder, E. Pomjakushina, L. Le Dreau, N. B. Christensen, O. F. Syljuåssen, B. Normand
and H. M. Rønnow,
Phys. Rev. B 89, 085113 (2014).
[23] Electronic and Magnetic Excitations in the “Half-Stuffed” Cu-O Planes of Ba2Cu3O4Cl2 Measured
by Resonant Inelastic X-Ray Scattering,
S. Fatale, C. G. Fatuzzo, P. Babkevich, N. E. Shaik, J. Pelliciari, X. Lu, D. E. McNally, T. Schmitt,
A. Kikkawa, Y. Taguchi, Y. Tokura, B. Normand, H. M. Rønnow and M. Grioni,
Phys. Rev. B 96, 115149 (2017).
[24] Giant Pressure-Dependence and Dimensionality Switching in a Metal-Organic Quantum
Antiferromagnet,
B. Wehinger, C. Fiolka, A. Lanza, R. Scatena, M. Kubus, A. Grockowiak, W. A. Coniglio, D. Graf,
M. Skoulatos, J.-H. Chen, J. Gukelberger, N. Casati, O. Zaharko, P. Macchi, K. W. Krämer, S.
Tozer, C. Mudry, B. Normand and Ch. Rüegg,
Phys. Rev. Lett. 121, 117201 (2018).
[25] Thermal Control of Spin Excitations in the Coupled Ising-Chain Material RbCoCl3,
M. Mena, N. Hänni, S. Ward, E. Hirtenlechner, R. Bewley, C. Hubig, U. Schollwöck, B. Normand,
K. W. Krämer, D. F. McMorrow and Ch. Rüegg,
Phys. Rev. Lett. 124, 257201 (2020).
[26] Triplons, Magnons, and Spinons in a Single Quantum Spin System: SeCuO3,
L. Testa, V. Surija, K. Prsa, P. Steffens, M. Boehm, B. Normand, H. M. Rønnow and I. Zivkovic,
unpublished (arXiv:2007.02972).
[27] Order by Disorder from Non-Magnetic Impurities in a Two-Dimensional Quantum Spin Liquid,
S. Wessel, B. Normand, M. Sigrist and S. Haas,
Phys. Rev. Lett 86, 1086 (2001).
[28] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[29] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[30] Nonmagnetic Impurities in the S = 3/2 Kagome Antiferromagnet,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[31] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2,
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
[32] High-dimensional Fractionalization and Spinon Deconfinement in Pyrochlore Antiferromagnets,
Z. Nussinov, B. Normand, C. D. Batista and S. A. Trugman,
Phys. Rev. B 75, 094411 (2007).
[33] Hubbard Model on the Pyrochlore Lattice: a 3D Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. Lett. 112, 207202 (2014).
[34] Fermionic Spinon and Holon Statistics in the Pyrochlore Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. B 93, 115122 (2016).
[35] Frustration and Entanglement in the t2g Spin-Orbital Model on the Triangular Lattice: Valence-Bond
and Generalized Liquid States,
B. Normand and A. M. Oleś,
Phys. Rev. B 78, 094427 (2008).
[36] Multicolored Quantum Dimer Models, Resonating Valence-Bond States, Color Visons, and the
Triangular-Lattice t2g Spin-Orbital System,
B. Normand,
Phys. Rev. B 83, 064413 (2011).
[37] Tensor Renormalization of Quantum Many-Body Systems using Projected Entangled Simplex States,
Z. Y. Xie, J. Chen, J. F. Yu, X. Kong, B. Normand and T. Xiang,
Phys. Rev. X 4, 011025 (2014).
[38] Heisenberg Antiferromagnet on the Husimi Lattice,
H. J. Liao, Z. Y. Xie, J. Chen, X. J. Han, H. D. Xie, B. Normand and T. Xiang,
Phys. Rev. B 93, 075154 (2016).
[39] Gapless Spin-Liquid Ground State in the S = 1/2 Kagome Antiferromagnet,
H. J. Liao, Z. Y. Xie, J. Chen, X. Kong, B. Normand and T. Xiang,
Phys. Rev. Lett. 118, 137202 (2017).
[40] Gapless Spin Liquid in the Kagome Heisenberg Antiferromagnet with Dzyaloshinskii-Moriya
Interactions,
C.-Y. Lee, B. Normand and Y.-J. Kao,
Phys. Rev. B 98, 224414 (2018).
[41] Frontiers in Frustrated Magnetism,
B. Normand,
Contemporary Physics 50, 4, 533 (2009).
[42] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[43] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in Staggered
Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[44] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 220402 (2011).
[45] Magnetization in Molecular Iron Rings,
B. Normand, X. Wang, X. Zotos and D. Loss,
Phys. Rev. B 63, 184409 (2001).
[46] Spin Dynamics and Coherent Tunnelling in the Molecular Magnetic Rings Fe6 and Fe8,
A. Honecker, F. Meier, D. Loss and B. Normand,
Eur. Phys. J. B 27, 487 (2002).
[47] Exchange Interactions and High-Energy Spin States in Mn12-acetate,
G. Chaboussant, A. Sieber, S. Ochsenbein, H.-U. Güdel, M. Murrie, A. Honecker, N. Fukushima
and B. Normand,
Phys. Rev. B 70, 104422 (2004).
[48] Exchange Constants and Spin Dynamics in Mn12-acetate,
A. Honecker, N. Fukushima, B. Normand, G. Chaboussant and H.-U. Güdel,
J. Mag. Mag. Mater. 290, 966 (2005).
[49] Spin-Charge Separation in Aharonov-Bohm Rings of Interacting Electrons,
K. Hallberg, A. A. Aligia, A. P. Kampf and B. Normand,
Phys. Rev. Lett. 93, 067203 (2004).
[50] Detection of Topological Transitions by Transport through Molecules and Nanodevices,
A. A. Aligia, K. Hallberg, B. Normand and A. P. Kampf,
Phys. Rev. Lett. 93, 076801 (2004).
[51] Quantum Phase Diagram of the Generalized Ionic Hubbard Model for ABn Chains,
M. E. Torio, A. A. Aligia, G. I. Japaridze and B. Normand,
Phys. Rev. B 73, 115109 (2006).
B. Normand and T. M. Rice,
Phys. Rev. B 54, 7180 (1996).
[2] Dynamical Properties of an Antiferromagnet near the Quantum Critical Point: Application to LaCuO2.5,
B. Normand and T. M. Rice,
Phys. Rev. B 56, 8760 (1997).
[3] Possible Superconductivity in the doped Ladder Compound La1-xSrxCuO2.5,
B. Normand, D. F. Agterberg and T. M. Rice,
Phys. Rev. Lett 82, 4296 (1999).
[4] Phase Diagram of the S = 1/2 Frustrated Coupled Ladder System,
B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 56, R5736 (1997).
[5] Magnetic Properties of the Coupled Ladder System MgV2O5,
P.Millet, C. Satto, J. Bonvoisin, B. Normand, K. Penc, M. Albrecht and F. Mila,
Phys. Rev. B 57, R5005 (1998).
[6] Magnetic Properties of (VO)2P2O7 from Frustrated Interchain Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 58, R14705 (1998).
[7] Magnetic Properties of (VO)2P2O7: Two-Plane Structure and Spin-Phonon Coupling,
G. S. Uhrig and B. Normand,
Phys. Rev. B 63, 134418 (2001).
[8] Nonlinear sigma Model Treatment of Quantum Antiferromagnets in a Magnetic Field,
B. Normand, J. Kyriakidis and D. Loss,
Ann. Phys. (Leipzig) 9, 133 (2000).
[9] Quantum Antiferromagnets in a Magnetic Field,
B. Normand,
Acta Phys. Polonica B 31, 3005 (2000).
[10] Magnon Dispersion in the Field-Induced Magnetically Ordered Phase of TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. Lett. 89, 077203 (2002).
[11] Pressure- and Field-Induced Magnetic Quantum Phase Transitions in TlCuCl3,
M. Matsumoto, B. Normand, T. M. Rice and M. Sigrist,
Phys. Rev. B 69, 054423 (2004).
[12] Quantum Magnets under Pressure: Controlling Elementary Excitations in TlCuCl3,
Ch. Rüegg, B. Normand, M. Matsumoto, A. Furrer, D. McMorrow, K. Krämer, H.-U. Güdel,
S. Gvasaliya, H. Mutka and M. Boehm,
Phys. Rev. Lett. 100, 205701 (2008).
[13] Universal Scaling at Field-Induced Magnetic Phase Transitions,
O. Nohadani, S. Wessel, B. Normand and S. Haas,
Phys. Rev. B 69, 220402 (2004).
[14] Quantum Statistics of Interacting Dimer Spin Systems,
Ch. Rüegg, B. Normand, M. Matsumoto, Ch. Niedermayer, A. Furrer, K. W. Krämer, H.-U. Güdel,
Ph. Bourges, Y. Sidis and H. Mutka,
Phys. Rev. Lett. 95, 267201 (2005).
[15] Multiple Magnon Modes and Consequences for the Bose-Einstein Condensed Phase in BaCuSi2O6,
Ch. Rüegg, D. F. McMorrow, B. Normand, H. M. Ronnow, S. E. Sebastian, I. R. Fisher, C. D. Batista, S. Gvasaliya, Ch. Niedermayer and J. Stahn,
Phys. Rev. Lett. 98, 017202 (2007).
[16] Multiple Magnetic Bilayers and Unconventional Criticality without Frustration in BaCuSi2O6,
S. Allenspach, A. Biffin, U. Stuhr, G. S. Tucker, S. Ohira-Kawamura, M. Kofu, D. J. Voneshen,
B. Normand, N. Laflorencie, F. Mila and Ch. Rüegg,
Phys. Rev. Lett. 124, 177205 (2020).
[17] Thermodynamics of the Spin Luttinger Liquid in a Model Ladder Material,
Ch. Rüegg, K. Kiefer, B. Thielemann, D. F. McMorrow, V. Zapf, B. Normand, M. B. Zvonarev,
P. Bouillot, C. Kollath, T. Giamarchi, S. Capponi, D. Poilblanc, D. Biner and K. W. Krämer,
Phys. Rev. Lett. 101, 247202 (2008).
[18] Field-Controlled Magnetic Order in the Quantum Spin-Ladder System (Hpip)2CuBr4,
B. Thielemann, Ch. Rüegg, K. Kiefer, H. M. Ronnow, B. Normand, P. Bouillot, C. Kollath,
E. Orignac, R. Citro, T. Giamarchi, A. M. Läuchli, D. Biner, K. W. Krämer, F. Wolff-Fabris,
V. Zapf, M. Jaime, J. Stahn, N. B. Christensen, B. Grenier, D. F. McMorrow and J. Mesot,
Phys. Rev. B 79, R020408 (2009).
[19] Direct Observation of Magnon Fractionalization in the Quantum Spin Ladder,
B. Thielemann, Ch. Rüegg, H. M. Ronnow, J.-S. Caux, A. M. Läuchli, B. Normand, D. Biner,
K. W. Krämer, H.-U. Güdel, J. Stahn, S. N. Gvasaliya, K. Habicht, K. Kiefer, M. Boehm,
D. F. McMorrow and J. Mesot,
Phys. Rev. Lett. 102, 107204 (2009).
[20] Complete Bond-Operator Theory of the Two-Chain Spin Ladder,
B. Normand and Ch. Rüegg,
Phys. Rev. B 83, 054415 (2011).
[21] Bound States and Field-Polarized Haldane Modes in a Quantum Spin Ladder,
S. Ward, M. Mena, P. Bouillot, C. Kollath, T. Giamarchi, K. P. Schmidt, B. Normand, K. W. Krämer,
D. Biner, R. Bewley, T. Guidi, M. Boehm, D. F. McMorrow and Ch. Rüegg,
Phys. Rev. Lett. 118, 177202 (2017).
[22] Quantum and Thermal Ionic motion, Oxygen Isotope Effect, and Superexchange Distribution
in La2CuO4,
P. S. Häfliger, S. Gerber, R. Pramod, V. I. Schnells, B. dalla Piazza, R. Chati, V. Pomjakushin,
K. Conder, E. Pomjakushina, L. Le Dreau, N. B. Christensen, O. F. Syljuåssen, B. Normand
and H. M. Rønnow,
Phys. Rev. B 89, 085113 (2014).
[23] Electronic and Magnetic Excitations in the “Half-Stuffed” Cu-O Planes of Ba2Cu3O4Cl2 Measured
by Resonant Inelastic X-Ray Scattering,
S. Fatale, C. G. Fatuzzo, P. Babkevich, N. E. Shaik, J. Pelliciari, X. Lu, D. E. McNally, T. Schmitt,
A. Kikkawa, Y. Taguchi, Y. Tokura, B. Normand, H. M. Rønnow and M. Grioni,
Phys. Rev. B 96, 115149 (2017).
[24] Giant Pressure-Dependence and Dimensionality Switching in a Metal-Organic Quantum
Antiferromagnet,
B. Wehinger, C. Fiolka, A. Lanza, R. Scatena, M. Kubus, A. Grockowiak, W. A. Coniglio, D. Graf,
M. Skoulatos, J.-H. Chen, J. Gukelberger, N. Casati, O. Zaharko, P. Macchi, K. W. Krämer, S.
Tozer, C. Mudry, B. Normand and Ch. Rüegg,
Phys. Rev. Lett. 121, 117201 (2018).
[25] Thermal Control of Spin Excitations in the Coupled Ising-Chain Material RbCoCl3,
M. Mena, N. Hänni, S. Ward, E. Hirtenlechner, R. Bewley, C. Hubig, U. Schollwöck, B. Normand,
K. W. Krämer, D. F. McMorrow and Ch. Rüegg,
Phys. Rev. Lett. 124, 257201 (2020).
[26] Triplons, Magnons, and Spinons in a Single Quantum Spin System: SeCuO3,
L. Testa, V. Surija, K. Prsa, P. Steffens, M. Boehm, B. Normand, H. M. Rønnow and I. Zivkovic,
unpublished (arXiv:2007.02972).
[27] Order by Disorder from Non-Magnetic Impurities in a Two-Dimensional Quantum Spin Liquid,
S. Wessel, B. Normand, M. Sigrist and S. Haas,
Phys. Rev. Lett 86, 1086 (2001).
[28] Absence of Effective Spins 1/2 Induced by Nonmagnetic Impurities in a Class of Low-Dimensional
Magnets
B. Normand and F. Mila,
Phys. Rev. B 65, 104411 (2002).
[29] Static Impurities in the Kagome Lattice: Dimer Freezing and Mutual Repulsion,
S. Dommange, M. Mambrini, B. Normand and F. Mila,
Phys. Rev. B 68, 224416 (2003).
[30] Nonmagnetic Impurities in the S = 3/2 Kagome Antiferromagnet,
A. Läuchli, S. Dommange, B. Normand and F. Mila,
Phys. Rev. B 76, 144413 (2007).
[31] Dzyaloshinskii-Moriya Anisotropy and Nonmagnetic Impurities in the S = 1/2 Kagome System
ZnCu3(OH)6Cl2,
I. Rousochatzakis, S. R. Manmana, A. M. Läuchli, B. Normand and F. Mila,
Phys. Rev. B 79, 214415 (2009).
[32] High-dimensional Fractionalization and Spinon Deconfinement in Pyrochlore Antiferromagnets,
Z. Nussinov, B. Normand, C. D. Batista and S. A. Trugman,
Phys. Rev. B 75, 094411 (2007).
[33] Hubbard Model on the Pyrochlore Lattice: a 3D Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. Lett. 112, 207202 (2014).
[34] Fermionic Spinon and Holon Statistics in the Pyrochlore Quantum Spin Liquid,
B. Normand and Z. Nussinov,
Phys. Rev. B 93, 115122 (2016).
[35] Frustration and Entanglement in the t2g Spin-Orbital Model on the Triangular Lattice: Valence-Bond
and Generalized Liquid States,
B. Normand and A. M. Oleś,
Phys. Rev. B 78, 094427 (2008).
[36] Multicolored Quantum Dimer Models, Resonating Valence-Bond States, Color Visons, and the
Triangular-Lattice t2g Spin-Orbital System,
B. Normand,
Phys. Rev. B 83, 064413 (2011).
[37] Tensor Renormalization of Quantum Many-Body Systems using Projected Entangled Simplex States,
Z. Y. Xie, J. Chen, J. F. Yu, X. Kong, B. Normand and T. Xiang,
Phys. Rev. X 4, 011025 (2014).
[38] Heisenberg Antiferromagnet on the Husimi Lattice,
H. J. Liao, Z. Y. Xie, J. Chen, X. J. Han, H. D. Xie, B. Normand and T. Xiang,
Phys. Rev. B 93, 075154 (2016).
[39] Gapless Spin-Liquid Ground State in the S = 1/2 Kagome Antiferromagnet,
H. J. Liao, Z. Y. Xie, J. Chen, X. Kong, B. Normand and T. Xiang,
Phys. Rev. Lett. 118, 137202 (2017).
[40] Gapless Spin Liquid in the Kagome Heisenberg Antiferromagnet with Dzyaloshinskii-Moriya
Interactions,
C.-Y. Lee, B. Normand and Y.-J. Kao,
Phys. Rev. B 98, 224414 (2018).
[41] Frontiers in Frustrated Magnetism,
B. Normand,
Contemporary Physics 50, 4, 533 (2009).
[42] Phase Diagram of the Heisenberg Spin Ladder with Ring Exchange,
V. Gritsev, B. Normand and D. Baeriswyl,
Phys. Rev. B 69, 094431 (2004).
[43] Low-Energy Properties of Anisotropic Two-Dimensional Spin-1/2 Heisenberg Models in Staggered
Magnetic Fields,
B. Xi, S. Hu, J. Z. Zhao, G. Su, B. Normand and X. Q. Wang,
Phys. Rev. B 84, 134407 (2011).
[44] Accurate Determination of the Gaussian Transition in Spin-1 Chains with Single-Ion Anisotropy,
S. Hu, B. Normand, X. Q. Wang and L. Yu,
Phys. Rev. B 84, 220402 (2011).
[45] Magnetization in Molecular Iron Rings,
B. Normand, X. Wang, X. Zotos and D. Loss,
Phys. Rev. B 63, 184409 (2001).
[46] Spin Dynamics and Coherent Tunnelling in the Molecular Magnetic Rings Fe6 and Fe8,
A. Honecker, F. Meier, D. Loss and B. Normand,
Eur. Phys. J. B 27, 487 (2002).
[47] Exchange Interactions and High-Energy Spin States in Mn12-acetate,
G. Chaboussant, A. Sieber, S. Ochsenbein, H.-U. Güdel, M. Murrie, A. Honecker, N. Fukushima
and B. Normand,
Phys. Rev. B 70, 104422 (2004).
[48] Exchange Constants and Spin Dynamics in Mn12-acetate,
A. Honecker, N. Fukushima, B. Normand, G. Chaboussant and H.-U. Güdel,
J. Mag. Mag. Mater. 290, 966 (2005).
[49] Spin-Charge Separation in Aharonov-Bohm Rings of Interacting Electrons,
K. Hallberg, A. A. Aligia, A. P. Kampf and B. Normand,
Phys. Rev. Lett. 93, 067203 (2004).
[50] Detection of Topological Transitions by Transport through Molecules and Nanodevices,
A. A. Aligia, K. Hallberg, B. Normand and A. P. Kampf,
Phys. Rev. Lett. 93, 076801 (2004).
[51] Quantum Phase Diagram of the Generalized Ionic Hubbard Model for ABn Chains,
M. E. Torio, A. A. Aligia, G. I. Japaridze and B. Normand,
Phys. Rev. B 73, 115109 (2006).
